Neural Supersampling and Denoising for Real-time Path Tracing

Creating realistic images has been a persistently challenging problem in computer graphics, especially when it comes to rendering scenes with complex lighting. Path tracing achieves photorealistic quality rendering by simulating the way light rays bounce around the scene and interact with different materials, but it also requires significant computation to generate clean images. This is where neural supersampling and denoising come into play. In this blog post, we describe how our neural supersampling and denoising work together to push the boundaries for real-time path tracing.

Math behind Rendering

Rendering equation [1] formulates outgoing radiance ($L_o$) leaving a surface point ($x$) as the sum of emitted radiance ($L_e$) and the fraction of incoming radiance ($L_i$) scattered by material ($f_r$) and geometric ($\overrightarrow{\omega_i} \cdot \overrightarrow{n}$) terms over a hemisphere ($\Omega$) centered around the surface point.

Monte Carlo integration is a stochastic technique used to estimate the integrals with random samples in the domain. Path tracing uses Monte Carlo integration to estimate the integral in the rendering equation with random ray samples cast from the virtual camera’s origin over all possible light paths scattered from surfaces. Path tracing is conceptually simple, unbiased and offers complex physically based rendering effects like reflections, refractions, and shadows for a variety of scenes

Figure 1. Photorealistic rendering by path tracing with 32768 samples per pixel. (Classroom rendered by AMD Capsaicin Framework [10].) – link to full-size image (4MB)

Noise in path tracing images

The randomness of samples in Monte Carlo integration inherently produces noise when the scattered rays do not hit the light source after multiple bounces. Hence, many samples per pixel (spp) are required to achieve high quality pixels in Monte Carlo path tracing, often taking a couple of minutes or hours to render a single image. Although the higher number of samples per pixel, the higher chance of less noise in an image, in many cases even with several thousands of samples it still falls short to converge to high quality and shows visually annoying noise.

Figure 2. Path tracing with 32768 samples per pixel could still show noise. (Evermotion Archinteriors rendered by AMD Capsaicin Framework [10].) – link to full-size image (2.3MB)

Reconstructing pixels in noisy rendering

Denoising is one of techniques to address the problem of the high number of samples required in Monte Carlo path tracing. It reconstructs high quality pixels from a noisy image rendered with low samples per pixel. Often, auxiliary buffers like albedo, normal, roughness, and depth are used as guiding information that are available in deferred rendering. By reconstructing high quality pixels from a noisy image within much shorter time than that full path tracing takes, denoising becomes an inevitable component in real-time path tracing.

Existing denoising techniques fall into two groups: offline and real-time denoisers, depending on their performance budget. Offline denoisers focus on production film quality reconstruction from a noisy image rendered with higher samples per pixel (e.g., more than 8). Real-time denoisers target denoising noisy images rendered with very few samples per pixel (e.g., 1-2 or less) within a limited time budget.

It is common to use noisy diffuse and specular signals as inputs to denoise them separately with different filters and composite the denoised signals to a final color image to better preserve fine details. Many real-time rendering engines include separated denoising filters for each effect, like diffuse lighting, reflection, and shadows for quality and/or performance. Since each effect may have different inputs and noise characteristics, dedicated filtering could be more effective.

Neural Denoising

Neural denoisers [3,4,5,6,7,8] use a deep neural network to predict denoising filter weights in a process of training on a large dataset. They are achieving remarkable progress in denoising quality compared to hand-crafted analytical denoising filters [2]. Depending on the complexity of a neural network and how it cooperates with other optimization techniques, neural denoisers are getting more attention to be used for real-time Monte Carlo path tracing.

A unified denoising and supersampling [7] takes noisy images rendered at low resolution with low samples per pixel and generates a denoised as well as upscaled image to target display resolution. Such joint denoising and supersampling with a single neural network gives an advantage of sharing learned parameters in the feature space to efficiently predict denoising filter weights and upscaling filter weights. Most performance gain is obtained from low resolution rendering as well as low samples per pixel, giving more time budget for neural denoising to reconstruct high quality pixels.

Current AMD research

We are actively researching neural techniques for Monte Carlo denoising with the goal of moving towards real-time path tracing on AMD RDNA™ 2 architecture or higher GPUs. Our research sets a few aims as follows:

• Reconstruct spatially and temporally outstanding quality pixels with fine details given extremely noisy images rendered with 1 sample per pixel.
• Use minimal input by taking a noisy color image as input instead of separated noisy diffuse and specular signals.
• Handle various noise from all lighting effects with a single denoiser instead of multiple denoisers for different effects.
• Support both denoising-only and denoising/upscaling modes from a single neural network for wider use cases.
• Highly optimized performance for real-time path tracing at 4K resolution.

With these goals, we research a Neural Supersampling and Denoising technique which generates high quality denoised and supersampled images at higher display resolution than render resolution for real-time path tracing with a single neural network. Inputs include a noisy color image rendered with one sample per pixel and a few guide buffers that are readily available in rendering engines, like albedo, normal, roughness, depth, and specular hit distance at low resolution. Temporally accumulated noisy input buffers increase the effective samples per pixel of noisy images. History output is also reprojected by motion vectors for temporal accumulation. The neural network is trained with a large number of path tracing images to predict multiple filtering weights and decides how to temporally accumulate, denoise and upscale extremely noisy low-resolution images. Our technique can replace multiple denoisers used for different lighting effects in rendering engine by denoising all noise in a single pass as well as at low resolution. Depending on use cases, a denoising-only output can be utilized, which is identical to 1x upscaling by skipping upscale filtering. We show a sneak peek of our quality results here.

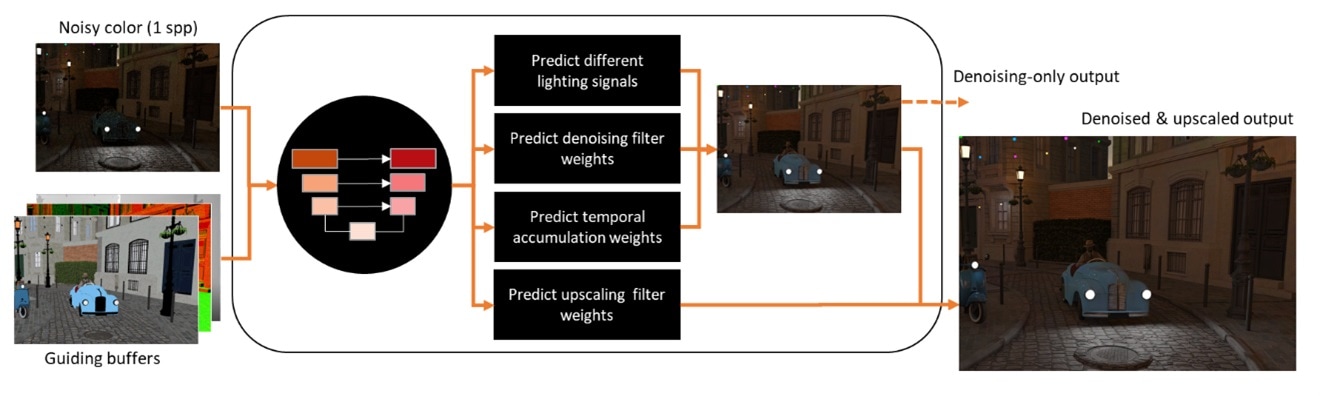
Figure 3. Workflow of our Neural Supersampling and Denoising. – link to full-size image (450K)

Figure 4. Denoised and upscaled result to 4K resolution for Bistro scene [9]. Input is a noisy image path traced with 1 sample per pixel in 1920×1080. – link to fullsize image (17.3MB)

Multi-branch and Multi-scale Feature Network

In our research, we devise a multi-branch and multi-scale U-Net to incorporate different characteristics in noisy color input and noise-free aliased guiding buffers while learning features for denoising and upscaling filtering. A guiding branch extracts features from auxiliary guiding buffers separated from a radiance branch for a noisy radiance input within a single feature extraction network. Since the auxiliary buffers are not noisy but just aliased, and contain redundant information, we structure relatively small and shallow layers for the guiding branch. This enables the creation of a lightweight feature extraction network.

To demonstrate the effectiveness of our feature extraction neural network, we compare our results with a few prior works. Below figures compare visual quality for denoising and upscaling (Figure 5) and denoising-only (Figure 6) with quality metrics (SSIM↑/LPIPS↓) calculated on a full resolution image. Our results show superior quality in preserving fine details. For temporal stability, see a video in Figure 7.

Further details are found in our paper [11] presented at I3D 2025.

Figure 5. Denoising and upscaling quality comparison in 4K resolution compared to prior works.

Figure 6. Denoising-only quality comparison in 1920x1080 resolution compared to the state-of-the art denoisers.

References

1. James T. Kajiya. 1986. The rendering equation. SIGGRAPH ‘86: Proceedings of the 13th annual conference on Computer graphics and interactive techniques. pp. 143–150.
2. Christoph Schied, Anton Kaplanyan, Chris Wyman, Anjul Patney, Chakravarty R. Alla Chaitanya, John Burgess, Shiqiu Liu, Carsten Dachsbacher, Aaron Lefohn, Marco Salvi. 2017. Spatiotemporal variance-guided filtering: real-time reconstruction for path-traced global illumination. Proceedings of High Performance Graphics, July 2017, pp 1–12.
3. Yuchi Huo, Sung-eui Yoon. 2021. A survey on deep learning-based Monte Carlo denoising. Comp. Visual Media, Volume 7, pp 169–185.
4. Steve Bako, Thijs Vogels, Brian Mcwilliams, Mark Meyer, Jan NováK, Alex Harvill, Pradeep Sen, Tony Derose, and Fabrice Rousselle. 2017. Kernel-predicting convolutional networks for denoising Monte Carlo renderings. ACM Transactions on Graphics, 36, 4, Article 97, pp 1–14.
5. Thijs Vogels, Fabrice Rousselle, Brian Mcwilliams, Gerhard Röthlin, Alex Harvill, David Adler, Mark Meyer, and Jan Novák. 2018. Denoising with kernel prediction and asymmetric loss functions. ACM Transactions on Graphics, 37, 4, Article 124, pp 1–15.
6. Mustafa Işık, Krishna Mullia, Matthew Fisher, Jonathan Eisenmann, and Michaël Gharbi. 2021. Interactive Monte Carlo Denoising using Affinity of Neural Features. ACM Transactions on Graphics, 40, 4, Article 37, pp 1–13.
7. Manu Mathew Thomas, Gabor Liktor, Christoph Peters, Sungye Kim, Karthik Vaidyanathan, and Angus G. Forbes. 2022. Temporally Stable Real-Time Joint Neural Denoising and Supersampling. Proceedings of the ACM on Computer Graphics and Interactive Techniques, 5, 3, Article 21, pp 1–22.
8. Martin Balint, Krzysztof Wolski, Karol Myszkowski, Hans-Peter Seidel, and Rafał Mantiuk. 2023. Neural Partitioning Pyramids for Denoising Monte Carlo Renderings. ACM SIGGRAPH 2023 Conference Proceedings, Article 60, pp 1–11.
9. Amazon Lumberyard. 2017. Amazon Lumberyard Bistro, Open Research Content Archive (ORCA).
10. AMD Capsaicin Framework.
11. Pawel Kazmierczyk, Sungye Kim, Wojciech Uss, Wojciech Kalinski, Tomasz Galaj, Mateusz Maciejewski, and Rama Harihara. 2025. Joint Denoising and Upscaling via Multi-branch and Multi-scale Feature Network. ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games.