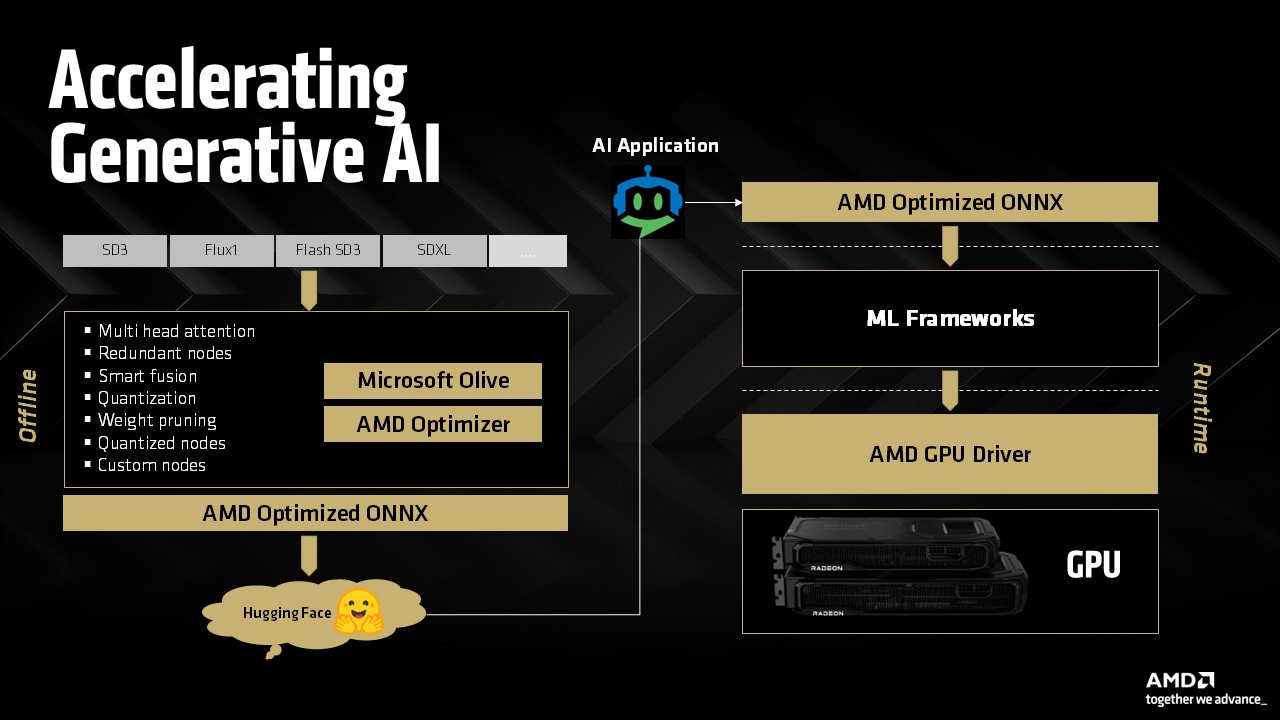
Accelerating Generative AI on AMD Radeon™ GPUs
Discover AMD-optimized ONNX models on Hugging Face for AMD Ryzen™ AI APUs and Radeon™ GPUs and incredible performance with the AMD Radeon RX 9000 Series' advanced AI accelerators.
As I recently went through a journey of learning how to make use of deep learning (in the context of computer graphics), I thought it would be good to write down some notes to help others get up to speed quickly. The goal of this article is to make the reader familiar with terms and concepts used in deep learning and to implement a basic deep learning algorithm. This should make it easier to study and understand other deep learning resources. This article comes with the source code and a sample application written in HLSL/DirectX 12 available at https://github.com/boksajak/Dx12NN.
Deep learning algorithms are powered by artificial neural networks. These are collections of interconnected neurons (also called units), usually organized into layers. When a neural network has large number of layers, we say that the network is deep, giving us a name deep learning. Each neuron has its inputs connected to other neurons via weighted connections, performs a simple computation over them, and passes its output to other neurons.
The type of neural network that we’re going to use in this article is called multilayer perceptron (MLP). It is relatively simple, but also powerful, and is widely used in practice (e.g., for neural radiance cache (NRC) and neural radiance fields (NeRFs)).
The MLP is constructed as follows:
Neurons are organized into layers, where first layer is called input layer, last layer is output layer and between them are hidden layers.
Each neuron has its inputs connected to outputs of all neurons in the previous layer. Therefore, we say that MLPs are fully connected networks, see the Figure 1 for an example.
This network architecture forms a directed acyclic graph, meaning that information only flows in one way, starting in the input layer and propagating through hidden layers to the output layer. We say that such network is a feedforward network.
Number of neurons and layers in the network determines how powerful the network is. Larger networks have the ability to learn more complex functions (we say that they have a larger capacity) but are typically more difficult to train and slower to evaluate. When designing a deep learning algorithm, we need to find a network size which is just right for the task. E.g., the NeRF paper uses MLP with 9 hidden layers consisting of 256 neurons each, and NRC uses 5 hidden layers with 64 neurons.
Note that these networks are small enough that they can be implemented in compute shaders and executed per pixel. In practice, some clever optimizations are necessary but it’s not impossible to have a deep learning algorithm running in real-time on current GPUs. It is also common to run neural networks using types with reduced precision, like FP16 or even smaller.
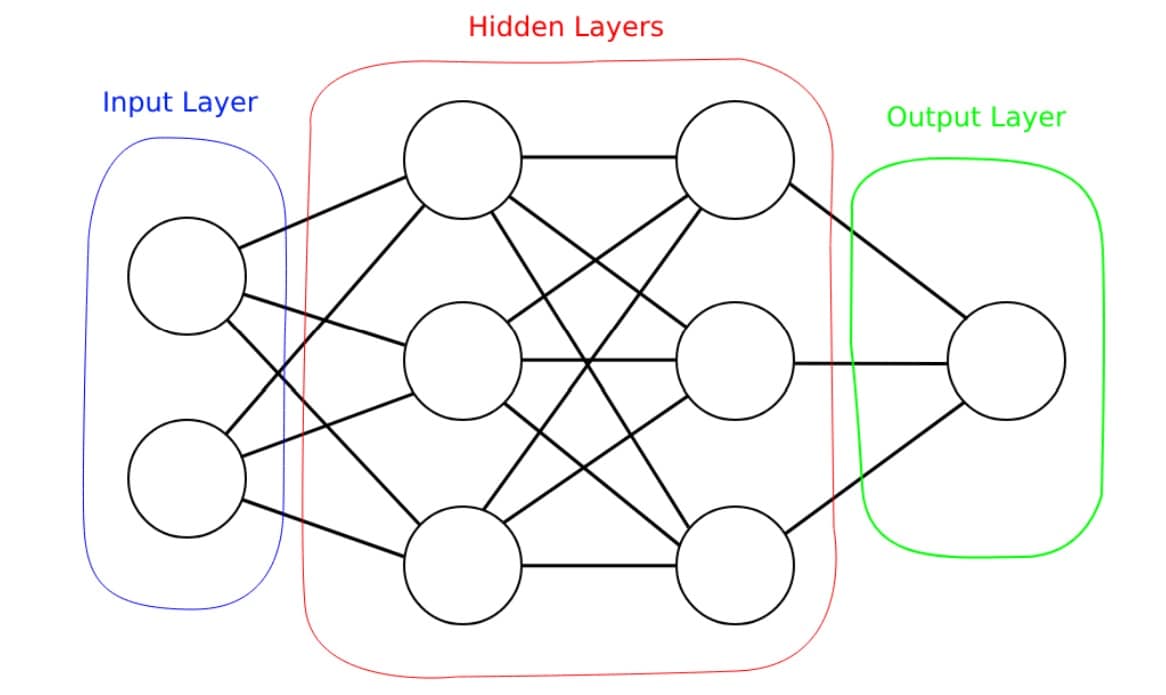
Figure 1 Architecture of a multi-layer perceptron neural network with 2 neurons in the input layer, 3 neurons per hidden layer and 1 neuron in the output layer.
All the computation that neural network does happens in the neurons. Output value of the neuron (also called its activation) is calculated as follows:
First, we sum up activations of all neurons from the previous layer connected to this neuron, weighted by the strength of the connection (this strength is also called the weight)
We add bias of the evaluated neuron to the sum. Bias is a per-neuron value which helps to represent non-linear relationships between network inputs and outputs. Without the bias, output of the network for zero input could only be a zero.
We apply the activation function to this sum to produce final neuron activation. This must be a non-linear function, which introduces another non-linearity between inputs and outputs. Usually, we use a simple function like (\max(0,x)). Without the activation function, outputs of the network could only be a linear combination of the inputs.
More formally, we can write neuron evaluation as:
where is the activation of the evaluated neuron, is the activation function, is the set of input neurons connected to the evaluated neuron, is the activation of the input neuron from previous layer, is the weight of the connection between neurons and and is the bias value of the evaluated neuron.
This means, that the output of the network for specific input is given by weights and biases and we need to set them accordingly to produce desired results. The process of adjusting weights and biases to make the network do what we want is called training.
Neural networks based on MLPs are usually used for one of two main tasks: classification and regression:
Classification: Categorizes the input into one (or more) predefined categories. These neural networks have one output neuron for each category and assign a probability of input belonging to each category as its output. E.g., we can have an input image of a hand-written digit and train the MLP to assign probability of the digit belonging into categories representing digits from 0 to 9. This exercise is a common “hello world” example in deep learning and there is a freely available set of images of hand-written digits called MNIST that can be used for it.
Regression: For given input, the regression calculates a continuous numerical value on the output (also called a prediction). The goal is to train the network to perform a desired mapping between inputs and output values. E.g., the NRC algorithm trains the network to map inputs like surface position and normal to radiance values.
In our sample application we will train the network to do regression, specifically it will learn to represent a 2D texture. We will provide UV coordinates of the texture as inputs, and we’ll expect RGB value of the corresponding texel on the output. We want it to learn the mapping:
For this example, our network will have 2 neurons in the input layer, corresponding to the and coordinates in the texture. On the output, we will have 3 neurons corresponding to the RGB values of the texel. In practice, it is common to encode the input into different representation. A naïve encoding which simply assigns inputs to input neurons as they are is called identity, and while it works, some clever encoding schemes usually perform much better. We’ll talk more about input encodings in section 4. Note that the input layer doesn’t perform any computation - instead of calculating activation of the neurons in the input layer, we simply assign input values as their activations.
Before we can use the MLP, it must be trained to perform our desired mapping well. Training is relatively complex and will be described in section 3, so let’s now assume that we have trained the network, obtained the correct weights and biases and we want to calculate the network output (prediction) for given input - this process is also called inference and because the information flows forward through the network, it’s sometimes also called the forward pass.
With the architecture of the MLP in mind, let’s now implement the inference. Before we start, it is useful to make it clear how we index data of the neural network in the arrays of weights, biases, activations etc. We need to store activations and biases per neuron, and the weights per connection between neurons. It is easy to make a mistake in indexing when working with graphs (our neural network is a graph), so let’s define a few rules for our indexing scheme:
We will index layers starting from 0: input layer has index 0, and output layer has index LAYER_COUNT - 1. Because the input layer doesn’t do any computation, it might be possible to skip it and start indexing from the first hidden layer, but we want to keep things clear and simple.
Connections between neurons will “belong” to the layer they are leading to. This means that layer 0 (input layer) doesn’t have any connections, and layer index LAYER_COUNT - 1 has connections from last hidden layer to the output layer.
Neurons in each layer are indexed from 0 to NUM_NEURONS_PER_LAYER
With this in mind, let’s define some helper functions to access data in global arrays:
uint getNeuronDataIndex(uint layer, uint neuron){ return neuronDataBaseOffsets[layer] + neuron;}
uint getConnectionDataIndex(uint layer, uint neuronFrom, uint neuronTo){ return connectionDataBaseOffsets[layer] + (neuronTo * neuronsPerLayer[layer - 1]) + neuronFrom;}Base offsets used in these functions are pre-calculated for each layer based on number of layers and number of neurons per layer in the network. Details can be found in the source code accompanying this article in the function createComputePasses.
With these in place, we can now implement a forward pass which:
Encodes input into activations array.
Iterates through all the layers where computation happens (all except the input layer).
a. Evaluates activation for each neuron in the layer.
Reads output from the activations array and returns it.
float activations[LAYER_COUNT * MAX_NEURONS_PER_LAYER];
// Identity encoding passes input as it isactivations[0] = input.x;activations[1] = input.y;
// Calculate activations for every layer, going forward through the MLP networkfor (uint layer = 1; layer < LAYER_COUNT; layer++){ const uint neuronCountCurrentLayer = neuronsPerLayer[layer]; const uint neuronCountPreviousLayer = neuronsPerLayer[layer - 1];
for (uint neuron = 0; neuron < neuronCountCurrentLayer; neuron++) { const uint neuronDataIndex = getNeuronDataIndex(layer, neuron);
// Evaluate neuron activation float neuronValue = nnBiases[neuronDataIndex];
// Accumulate weighted contribution from all neurons connected to this neuron in previous layer for (uint previousNeuron = 0; previousNeuron < neuronCountPreviousLayer; previousNeuron++) { const uint weightDataIndex = getConnectionDataIndex(layer, previousNeuron, neuron); const uint previousNeuronDataIndex = getNeuronDataIndex(layer - 1, previousNeuron);
neuronValue += nnWeights[weightDataIndex] * activations[previousNeuronDataIndex]; }
activations[neuronDataIndex] = ACTIVATION_FUNCTION(neuronValue); }}
const uint outputLayerActivationIndex = getNeuronDataIndex(LAYER_COUNT - 1, 0);const float3 result = float3(activations[outputLayerActivationIndex + 0], activations[outputLayerActivationIndex + 1], activations[outputLayerActivationIndex + 2]);Note that our code has allocated an array called activations where we store activations of all neurons during the forward pass. But for inference we only need to store activations of 2 layers at any time: the one that we are evaluating and the previous layer. As an optimization, we can allocate two smaller arrays with the size NUM_MAX_NEURONS_PER_LAYER and ping-pong between them. However, during the training we will need to store activations for all neurons from the forward pass to perform a backpropagation pass.
In the previous code listing, we have used the macro called ACTIVATION_FUNCTION in the place where we want to evaluate the activation function. Let’s now define it - remember that this must be a non-linear function, but we can pick any function assuming that it is differentiable (it has a derivative). The derivative will be needed for training.
Some of the functions commonly used are ReLU (rectified linear unit), leaky ReLU and sigmoid:
Even though ReLU and leaky ReLU are very simple, they work well and are widely used, e.g., by both NeRF and NRC papers. The 0.01 value (slope) in leaky ReLU implementation is a variable and you can experiment with different values. Usually, the whole network uses the same activation function, but it is not uncommon for output layer to have a different function than hidden layers.
Let’s now look at derivatives of these functions:
Note: the derivative of ReLU and leaky ReLU is undefined at point zero, because the function is discontinuous there, but in practice we must use a value of 0 in that point.
For our sample application, we use leaky ReLU by default. Sigmoid function is also available, but the training takes a much longer time compared to ReLU and leaky ReLU.
In this article, we implement neural network training based on a common supervised learning method. Supervised learning means that we evaluate the neural network on inputs for which we know correct outputs that we’d like to get, and we adjust it to give us results closer to desired outputs. Each input is called a sample or an example, and all inputs available for training are called a training set.
For each sample from the training set, we start by comparing network’s prediction to the correct output using a cost function. This function tells us how good the prediction was (lower is better). Then, we will update weights and biases in a way that minimizes this cost function. This is done using an algorithm called gradient descent. The gist of it is that we first calculate how the cost function changes if we change individual weights and biases, and then we adjust them in a direction that lowers the cost. In the following text, we will often refer to “weights and biases”, but I’m only going to write “weights” to keep the text more readable. Keep in mind that what applies to weights also applies to biases here.
To know how to adjust the weights to lower the cost we need to calculate a value for each weight that tells us how the cost function changes when that specific weight changes. These are called partial derivatives of a cost function wrt. the weight. The vector of all partial derivatives of our weights is called a gradient.
Now we can imagine the cost function as a multi-dimensional surface. The gradient points in a direction where the cost function rises most steeply. We can think about stochastic descent as a ball rolling down the hill on this surface (position of the ball is given by the current network state and the cost function value). We want to get the ball as low as possible to minimize the cost. By calculating gradients (which point up the hill on this surface), and moving in opposite direction, we basically roll the ball downhill to some local minimum. Gradient is calculated using the algorithm called backpropagation which we’ll discuss in section 3.5. The process of adjusting the weights is also called an optimization of the network.
Once we have calculated the gradient, we can simply nudge the weights in an opposite direction by some small amount. This method of minimizing the cost function will eventually get us to a local minimum of the cost function. Note that this method doesn’t find a global minimum (unless it gets very lucky), but in practice this is not a huge issue for highly dimensional problems which typically have many local minima, with values similar to the global minimum.
We repeat this process many times to iteratively lower the cost. In each step, weights are not adjusted by the whole magnitude of the gradient, but we first multiply it by a small number (e.g., 0.0001) to take smaller steps. This multiplication constant is called a learning rate, and it tells us how fast the gradient descent should progress along the path to the local minimum. Without the learning rate, gradient descent would be taking very large steps, while being unstable and oscillating around the local minimum. Picking a right learning rate is critical in order to ensure that training will be stable, but also sufficiently fast. In practice, we will often have an adaptive learning rate. We will start with highest learning rate, and we lower it after each training step according to some schedule (e.g., linearly or exponentially). In practice, more advanced optimizers are used to adjust the weights, like the Adam optimizer that we’ll describe in section 5.
Learning rate is what we call a hyperparameter - it’s a parameter of a neural network implementation which is not learned by training, but rather set by a user. More advanced training algorithms have many hyperparameters. Important thing to realize is that we don’t always have to set hyperparameters manually, but we can have other optimizing algorithm (even one based on machine learning) finding the optimal values of hyperparameters for us.
Let’s now look at the overview of how the whole training algorithm with gradient descent works. The single training step does the following:
Evaluate the network for each sample from a training set.
a. Calculate a cost function for each sample, using the calculated and expected outputs.
b. Calculate a gradient for each sample.
Average the gradients calculated in step 1b (so that we obtain one partial derivative value for each weight and bias in the network).
Optimize the network: scale the averaged gradient by learning rate and subtract it from the current weights to obtain new weights.
Repeat from step 1.
Going through all the inputs in the training set is called an epoch and we’ll need many epochs before the network converges to a local minimum of a cost function. Going through all the inputs in every step can be cumbersome, as the algorithm goes through the whole data set every time. As an optimization, we can use a modified method called stochastic gradient descent (SGD).
In practice, we don’t need to go through the whole training set before updating the weights. We can split the training set into a number of random subsets (batches) and update weights after processing every batch. This way, we will perform weight updates more often, achieving faster learning and consuming less memory. The downside is that our gradient is not so precise anymore and it doesn’t guide us to the local minimum along the shortest path. But if our subsets are good representatives of a whole training set, this doesn’t pose a big problem in practice. The process of using batches is also called mini-batching. SGD introduces at least two new hyperparameters - batch size and number of epochs to perform per training step.
Remember that our sample application wants to train the network to represent a 2D image, mapping UV coordinates to RGB texel values. We will use SGD for that, taking a batch of 2048 samples per each training step, and we’ll take one training step per frame. If we had to go through all the texels in every training step, the memory requirements and runtime performance would be unusable. For our example, we don’t even need to store the training set explicitly, we can simply generate desired number of random samples in run-time by randomly sampling the texture.
The training as described above can in theory run indefinitely - improving the predictions and getting the cost function lower and lower. It is unlikely that it will ever reach zero, due to constraints of the neural network architecture and learning algorithm. In practice, we have to decide at some point that training has reached the best state possible and stop. At first it seems that we can set a threshold for the cost function that we want to reach and stop after achieving it, but there is a problem: If we only measure the cost on training data, we won’t know how it will perform on real world data it has not seen before. This is the problem of generalization. We want the network to perform well also on general data that it has not seen during the training. As the training progresses, the neural network will start remembering the training data, instead of learning some general relationships between inputs and outputs, and it will fail to generalize well to new data. We also say that our model is overfitting in this case.
To solve this, we should also track a validation error measured on a data set which is separate from the training set. This error will be high at the beginning (just like the training error), and will get lower with training, but after some time it will start to rise again. This rise happens at the point when neural network stops generalizing well to data not seen by training, and it is the point when we should stop training. It is common to create a validation set from the training data that we have available by splitting it into 80% training set and 20% validation set. It is, however, necessary to make sure that training and validation sets don’t mix. This method of stopping the training when validation error start rising is called early stopping.
Note that some algorithms like NRC don’t ever stop training - they run in real time to make sure that neural network adapts to changes in the scene. Our sample application also runs the training continuously because for our use case, the generalization is not a problem, we simply want it to learn one input image as good as it can.
For our sample application, we will use a mean squared error (MSE) as a cost function:
There are also other cost functions used in practice, like the L1 loss or L2 loss. We can use any function which gives lower score to better outcomes, but the function must have a derivative, which we’ll need for calculating the gradient.
Cost function is often also called a loss function and its value simply a loss. Cost functions can also have additional regularization terms which impose additional cost, e.g., for case when weights and biases get very large (this is called weight decay). This will force the weights to be as small as possible, which can help to prevent overfitting.
Let’s now discuss how we calculate the gradient using the backpropagation algorithm. As the name suggests, the algorithm starts at the output layer and continues backwards through the network. It is therefore also called the backward pass through the network.
The goal of this algorithm is to calculate partial derivative for each weight and bias wrt. cost function, which we designate as and . Before we start let’s formally define some things we’ll need to calculate those partial derivatives:
where is the output of the neuron without applying activation function, is a weight of the connection to the neuron , is the activation of connected neuron , is the bias value, is the output with activation function applied, and is the activation function.
So how can we calculate these partial derivatives knowing the cost function value? The trick is to split calculations of and into several derivatives which are easier to calculate and combine them using a chain rule. Let’s start with the simplest, which is . This is the same as , and is also called an error of the neuron:
We have now split into two simpler derivatives and . For the neuron in the output layer, is just telling us how the cost changes when its activation changes. This is equal to the partial derivative of the cost function with respect to evaluated neuron. When we use the MSE cost function, this derivative is:
where is the constant coming from the derivation of MSE (in our sample where target is a 3-component vector, the is equal to ). In code, we can ignore this constant as it would only scale the whole gradient by the same number, and the gradient scale is already controlled by learning rate.
Next is the value. This tells us how the output of the neuron changes when we apply the activation function. This is simply a derivative of the activation function which we described in section 2.4.
We have now calculated the partial derivative of the bias term of the neuron in the output layer, and we can use it to adjust this neuron’s bias. Next, let’s look at the derivatives of weights connecting to this neuron, splitting it again like:
The term is the same error that we calculated before, and the new term tells us how the neuron value without activation function changes when we change that weight. This is a partial derivative of wrt. , which just boils down to the activation of the connected neuron:
While these derivatives look intimidating at first, they boil down to a very simple calculation:
With this knowledge, we can now implement gradient calculation for the output layer:
// Gradient of biasconst uint neuronDataIndex = getNeuronDataIndex(LAYER_COUNT - 1, neuron);
const float neuronActivation = activations[neuronDataIndex];const float dCost_O = (neuronActivation - target[neuron]);const float dO_Z = ACTIVATION_FUNCTION_DERIV(neuronActivation);const float dCost_Z = dCost_O * dO_Z;errors[neuronDataIndex] = dCost_Z;InterlockedAdd(gradientBiases[neuronDataIndex], packFloat(dCost_Z));
// Gradient of weightsfor (uint previousNeuron = 0; previousNeuron < neuronCountPreviousLayer; previousNeuron++){ const uint previousNeuronDataIndex = getNeuronDataIndex(LAYER_COUNT - 2, previousNeuron); const float dCost_weight = dCost_Z * activations[previousNeuronDataIndex]; const uint weightIndex = getConnectionDataIndex(LAYER_COUNT - 1, previousNeuron, neuron); InterlockedAdd(gradientWeights[weightIndex], packFloat(dCost_weight));}What remains is to calculate the same partial derivatives for the hidden layer, which is just slightly more complicated. Because the neurons in the hidden layer are connected to other neurons, their values are not dependent on the cost function directly, but on the connected neurons. Specifically:
Where is the j-th neuron connected to the output of evaluated neuron , is the error of the j-th neuron evaluated previously, and tells us how the output of neuron without activation function changes when the output of the evaluated neuron changes. This is a derivative of wrt. , so simply a strength of the connection between the neurons:
The code for hidden layer gradient is almost the same, except for the calculation, which is:
float dCost_O = 0.0f;for (uint nextNeuron = 0; nextNeuron < neuronCountNextLayer; nextNeuron++){ const uint weightIndex = getConnectionDataIndex(layer + 1, neuron, nextNeuron); const uint nextNeuronDataIndex = getNeuronDataIndex(layer + 1, nextNeuron); dCost_O += (errors[nextNeuronDataIndex] * nnWeights[weightIndex]);}Notice that in order to implement this, we had to store errors of the previously evaluated neurons. We can say that the error is propagating backwards through the neural network, giving this algorithm its name - backpropagation. We also need to store activations for all neurons, which was not necessary for the forward pass.
The code sample implements training as described above running on the GPU using Dx12 compute shaders. The whole training runs in 2 main kernel dispatches: gradient calculation and optimization. For gradient calculation, we run as many threads in parallel as we have training examples in the batch. Each thread generates a training example by randomly sampling a reference texture. Then it runs the forward pass to evaluate activations for the whole network, followed by the backpropagation pass to calculate the gradient. You may have noticed in the previous listings that we use InterlockedAdd operation to store the gradient. This is because we are interested in average gradient for all training examples in the batch, so we can add them all up and then divide the sum by the batch size before using it. The code for a gradient calculation step is:
// Initialize random numbers generatoruint rng = initRNG(LaunchIndex, uint2(1, 1), gData.frameNumber);
// Generate a random input (UV coordinates in the image)const float2 uvs = float2(rand(rng), rand(rng));
// Load target value to learn for this input from reference imageconst float3 target = targetTexture[uvs * float2(gData.outputWidth - 1, gData.outputHeight - 1)].rgb;
// First run forward pass to evaluate network activations for given inputfloat activations[LAYER_COUNT * MAX_NEURONS_PER_LAYER];forwardPass(uvs, activations);
// Run backpropagation on current network statebackpropagation(target, activations);The next step - optimization - runs once after calculating gradient for every batch, reads the gradient and adjusts the weights and biases accordingly.
There is one important aspect of training we haven’t covered yet and that’s the initial state of the network before we start the training. Initial weights and biases influence where our training starts and how fast can it approach the optimal solution, so a good initialization strategy is desirable. If we used some constant for all initial weights (e.g., zero or one), all activations and their gradients would be the same - the network wouldn’t be learning anything as every neuron would follow the same learning path (assuming we have a deterministic learning algorithm).
Because of this, we want to start with different initial weight and bias setting for each neuron to “break the symmetry”. Therefore, we initialize the network with some small random numbers centered around zero. We can take these numbers, e.g., from the uniform or normal distribution. To do that we must pick a range in which to generate random numbers, and in case of normal distribution also the standard deviation. These can either be hyperparameters tuned manually, or better, we can use one of the common strategies for setting them automatically. Such strategies are, e.g., LeCun uniform, Xavier uniform and their variations using normal distribution. These have been introduced in paper Understanding the difficulty of training deep feedforward neural networks.
In our code sample we use the Xavier uniform initialization. It generates weights using a uniform random distribution within the range , where is dependent on number of neurons in layers that the weight is connecting:
Random initial values for weights are enough to break the symmetry and ensure proper learning, and therefore it is common to initialize biases to zeroes, or some small constant.
So far, we have only used the identity input encoding. Meaning, we have simply passed our UV coordinates into two input neurons. In this section we are going to explore a more advanced input encoding, the frequency encoding, which greatly improves performance for our sample application.
This encoding was described in the NeRF paper under the name “positional encoding”, but I see it’s often referred to as the “frequency encoding”. Idea is to transform the input into higher-dimensional space using the following formula:
where is the input value we want to encode, is the number of frequencies we want to use (e.g., 8) and is a vector of encoded values. Note that with this encoding, we have greatly increased number of input neurons. For our sample application with 2 input values, and 8 frequencies, we get 32 input neurons.
Having inputs in higher-dimensional space will make it easier for neural network to discover more complex relationships between inputs and outputs. Implementation of this encoding can be found in the sample code in function called frequencyEncoding.
In the deep learning literature, you will often encounter a one-hot encoding. This is a very simple encoding where input is encoded into a vector of values, where only a single entry is 1, and others are 0 (we say that one value is hot). E.g., we can encode a fact that object belongs to certain category by having a vector of values representing each category, and setting value 1 for the selected category, while zeroing out others.
For more advanced encodings, I recommend looking at the one-blob encoding, introduced in Neural Importance Sampling paper, which extends one-hot encoding to have multiple entries activated, instead of just one. This essentially activates or shuts down parts of the network, depending on the input value.
Another useful encoding is a hash-grid encoding introduced in Instant Neural Graphics Primitives with a Multiresolution Hash Encoding paper.
So far, we have applied gradients during the training using a very simple way - we just multiplied it by the learning rate and subtracted it from current weights and biases. While this works, it is not optimal for several reasons: fixed learning rate is usually suboptimal at the beginning, when we want to take larger steps to proceed faster, but it is also suboptimal at the end, when it can oscillate around the optimal solution because the fixed step is too large to get into the valley of local minimum. In practice, we want to use an adaptive learning rate instead.
In this section we implement an improved optimizer called Adam (adaptive moment estimation), described in the paper Adam: A Method for Stochastic Optimization. Adam adds two ingredients to the optimization process: adaptive learning rate and momentum.
We have described adaptive learning rate before, so let’s now look at the momentum. Remember our “ball rolling” example where we stated that minimizing the cost function is like rolling the ball on its surface to find a lowest point. Just like in real world, where the ball has certain momentum, we can add momentum to our algorithm by taking into consideration the gradients in previous steps and applying a weighted average of them, instead of just latest gradients. This way, we progress to the optimum faster and we have a higher chance of escaping shallow valleys with local minima to find even lower local minimum.
Adam optimizer works by tracking the first and second moments (mean and variance) of the gradient. This means that for each weight and bias, we have to track mean and variance of their partial derivatives. They are averaged over time and their decay is controlled by new hyperparameters and . The adjustment done to weight or bias is calculated using its gradient, mean, and variance in the following way:
// Update mean and variance for this training step
mean = lerp(gradient, mean, gData.adamBeta1);variance = lerp((gradient * gradient), variance, gData.adamBeta2);
// Calculate weight (or bias) adjustmentconst float correctedMean = mean / (1.0f - gData.adamBeta1T);const float correctedVariance = variance / (1.0f - gData.adamBeta2T);const float weightAdjustment = -gData.learningRate * (correctedMean / (sqrt(correctedVariance) + gData.adamEpsilon));The updated mean and variance are stored next to weights and biases. Note that we still have to set a base learning rate when using this algorithm, the paper suggests a value of 0.001. In practice, the default values suggested in the paper for and are used as well. The default value for which prevents division by zero is . Values and are derived from and and adjusted after each training step as follows:
adamBeta1T = pow(adamBeta1, training_steps + 1);adamBeta2T = pow(adamBeta2, training_steps + 1);While the method for training described so far is fairly robust and efficient, there are several problems which we can encounter in practice, let’s briefly discuss some of them:
Insufficient training data: when we have low amount of training data, or when the batch size of stochastic gradient descent is too low, we won’t be able to find a stable solution that generalizes well. Make sure to have sufficient data to get into local minimum of the cost function.
Non-deterministic data: So far, we assumed that there is a deterministic relationship between the training inputs and target outputs. Breaking this assumption by having some random values can make it hard or impossible for training to converge.
Wrong learning rate: Having a learning rate too small will cause the training to proceed very slowly, while having it too large can make the training unstable.
Vanishing gradients: For deep networks, gradients in certain layers can become very small, slowing down or even stopping the training. This happens because for typical activation functions, large changes on some inputs can only cause small changes (or no changes) of the output. E.g., the negative part of the leaky ReLU outputs very small values. In this case, partial derivatives become smaller and smaller, and training doesn’t change the weights much. One of the possible solutions is to use different activation functions.
Exploding gradients: The opposite problem happens when gradients get very large and cause instability. As a solution, we can clamp gradients to some threshold value, limiting the rate at which they can change weights and biases - this is called the gradient clipping.
There is a lot more to deep learning than what I described so far in this article. Before we wrap up, I want to mention at least two topics worth studying next, that you will encounter often when reading deep learning papers focused on computer graphics: auto-encoders and convolutional networks.
Auto-encoder is a type of neural network consisting of encoder and a decoder. Encoder translates input data into more compact representation (in latent space) and decoder is used to decompress it to original representation. It can be used for applications like data compression, denoising and image reconstruction.
Convolutional networks (CNNs) are specialized networks used mostly in image processing. They contain 2 types of hidden layers: convolutional layers intended to detect certain features in images, and pooling layers which downsample intermediate results into more compact representation.
While I was first learning about deep learning, I found great insight in the paper titled “Multilayer Feedforward Networks are Universal Approximators” from 1989. It says that MLPs with at least one hidden layer are universal approximators, meaning they can approximate any function to a degree allowed by the network capacity. It also says that failure to approximate given function can be attributed to inadequate learning, insufficient network capacity, or non-deterministic relation between network inputs and outputs. In practice, we can therefore use MLPs to replace parts of our algorithms which contain difficult functions mapping data from one space to another.
In this article, I have described a few concepts and algorithms used in deep learning that I found most interesting for my use case (representing an image using an MLP), but there is much more to explore. With the knowledge provided here, I hope that you’ll have more fun reading deep learning papers and resources and implement your own deep learning ideas.
I recommend looking at the book Deep Learning: A Visual Approach by Glassner, the book Deep Learning by Goodfellow et al. which is freely available online, deep learning videos by 3Blue1Brown, neural network blogs by demofox, paper titled “Deep learning” by LeCun et al. from 2015, and graphics papers such as NeRF and NRC. When implementing neural networks, I recommend reading an article How to accelerate AI applications on RDNA 3 using WMMA for insights how to use AI accelerating instructions of current GPUs. Finally, I recommend experimenting with libraries like pyTorch which enable much faster prototyping, than implementing everything from scratch.
I want to thank Daniel Meister for helpful comments and suggestions.
This blog was originally published by Jakub at https://boksajak.github.io/blog/DeepLearning.
