AMD FidelityFX™ Parallel Sort
AMD FidelityFX Parallel Sort makes sorting data on the GPU quicker, and easier. Use our SM6.0 compute shaders to get your data in order.
On this page
Quaternion defined Q:a+bi+cj+dk=(r,v)=(Qw,Qx,Qy,Qz)
1−2(Qy2+Qz2)2(QxQy−QzQw)2(QxQz+QyQw)02(QxQy+QzQw)1−2(Qx2+Qz2)2(QyQz−QxQw)02(QxQz−QyQw)2(QyQz+QxQw)1−2(Qx2+Qy2)00001Axis angle defined U:cos(θ)+sin(θ)(u^x,u^y,u^z)
where :∣∣u^∣∣=1
(1−c)u^x2+c(1−c)u^xu^y−su^z(1−c)u^xu^z+su^y0(1−c)u^xu^y+su^z(1−c)u^y2+c(1−c)u^yu^z−su^x0(1−c)u^xu^z−su^y(1−c)u^yu^z+su^x(1−c)u^z2+c00001Plane defined P:ax+by+cz+d=0
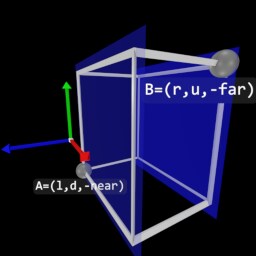
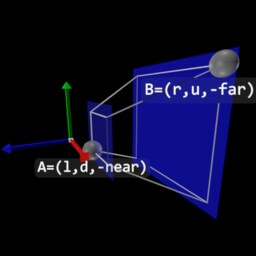
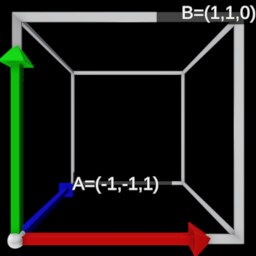
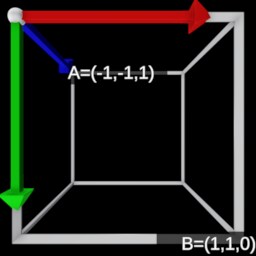
1−2a2−2ab−2ac−2ad−2ab1−2b2−2bc−2bd−2ac−2bc1−2c2−2cd0001l - left coordinate of the orthographic frustum
r - right coordinate of the orthographic frustum
b - bottom coordinate of the orthographic frustum
t - top coordinate of the orthographic frustum
n - distance to the near plane of the orthographic frustum
f - distance to the far plane of the orthographic frustum
w - width of the near plane of the orthographic frustum
h - height of the near plane of the orthographic frustum
| View Space | Left-handed NDC Space | Right-handed NDC Space | |
|---|---|---|---|
 |  | 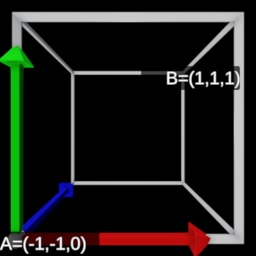 | 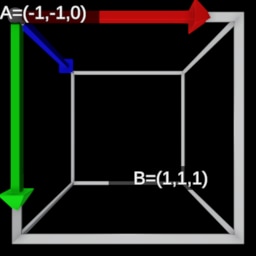 |
| View Space | Left-handed NDC Space | Right-handed NDC Space | |
|---|---|---|---|
 |  | 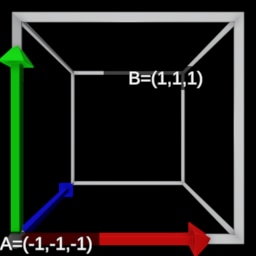 | 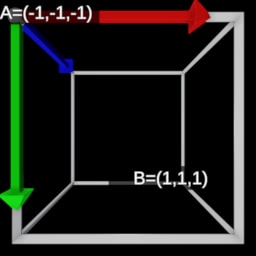 |
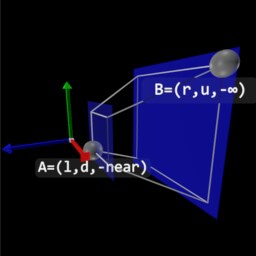
l - left coordinate of the perspective frustum
r - right coordinate of the perspective frustum
b - bottom coordinate of the perspective frustum
t - top coordinate of the perspective frustum
n - distance to the near plane of the perspective frustum
f - distance to the far plane of the perspective frustum
w - width of the near plane of the perspective frustum
h - height of the near plane of the perspective frustum
α - angle between of left and right frustum planes of the perspective frustum
β - angle between of top and bottom frustum planes of the perspective frustum
| View Space | Left-handed NDC Space | Right-handed NDC Space | |
|---|---|---|---|
 |  |  |  |
| View Space | Left-handed NDC Space | Right-handed NDC Space | |
|---|---|---|---|
 |  |  |  |
| View Space | Left-handed NDC Space | Right-handed NDC Space | |
|---|---|---|---|
 |  |  |  |
| View Space | Left-handed NDC Space | Right-handed NDC Space | |
|---|---|---|---|
 |  |  |  |
| View Space | Left-handed NDC Space | Right-handed NDC Space | |
|---|---|---|---|
 |  |  |  |
| View Space | Left-handed NDC Space | Right-handed NDC Space | |
|---|---|---|---|
 |  |  |  |
| View Space | Left-handed NDC Space | Right-handed NDC Space | |
|---|---|---|---|
 |  |  |  |
| View Space | Left-handed NDC Space | Right-handed NDC Space | |
|---|---|---|---|
 |  |  |  |
l - left coordinate of the orthographic frustum
r - right coordinate of the orthographic frustum
b - bottom coordinate of the orthographic frustum
t - top coordinate of the orthographic frustum
n - distance to the near plane of the orthographic frustum
f - distance to the far plane of the orthographic frustum
w - width of the near plane of the orthographic frustum
h - height of the near plane of the orthographic frustum
jx - jitter in NDC space in the x-direction
jy - jitter in NDC space in the y-direction
l - left coordinate of the perspective frustum
r - right coordinate of the perspective frustum
b - bottom coordinate of the perspective frustum
t - top coordinate of the perspective frustum
n - distance to the near plane of the perspective frustum
f - distance to the far plane of the perspective frustum
w - width of the near plane of the perspective frustum
h - height of the near plane of the perspective frustum
jx - jitter in NDC space in the x-direction
jy - jitter in NDC space in the y-direction
α - angle between of left and right frustum planes of the perspective frustum
β - angle between of top and bottom frustum planes of the perspective frustum
at - position of the point at which the camera will be pointing at
eye - position of the camera
up - “Up” direction of the camera
C - “Forward” vector
A - “Right” vector
B - “Up” vector
C=∥at−eye∥at−eye A=up×C B=C×A
AxBxCx−(A⋅eye)AyByCy−(B⋅eye)AzBzCz−(C⋅eye)0001dir - desired direction of the camera
up - “Up” direction of the camera
C - “Forward” vector
A - “Right” vector
B - “Up” vector
C=dir A=up×C B=C×A
AxBxCx−dot(A,eye)AyByCy−dot(B,eye)AzBzCz−dot(C,eye)0001Plane defined P:Ax+By+Cz+D=0
Light position L:(Lx,Ly,Lz)
where w=0 for direction light
w=1 for point light
L=(Lx,Ly,Lx,w) P=(A,B,C,D) k=P⋅L
k−PxLx−PxLy−PxLz−PxLw−PyLxk−PyLy−PyLz−PyLw−PzLx−PzLyk−PzLz−PzLw−PdLx−PdLy−PdLzk−PdLw