This is the first of a series of posts expanding on the ideas presented at GDC in the Advanced Techniques and Optimization of VDR Color Pipelines talk. This post details generation of symmetric grain ideal for traditional transfer functions like sRGB.

Below is the original photograph used in the dithering section of the talk. The photograph was chosen for a mix of smooth and detailed areas in combination with hard-to-quantize desaturated colors.

Now showing quantization to 8 steps in sRGB without addition of any grain. Quantization is nearest linear distance (which has a visual advantage over nearest non-linear difference for small numbers of steps).

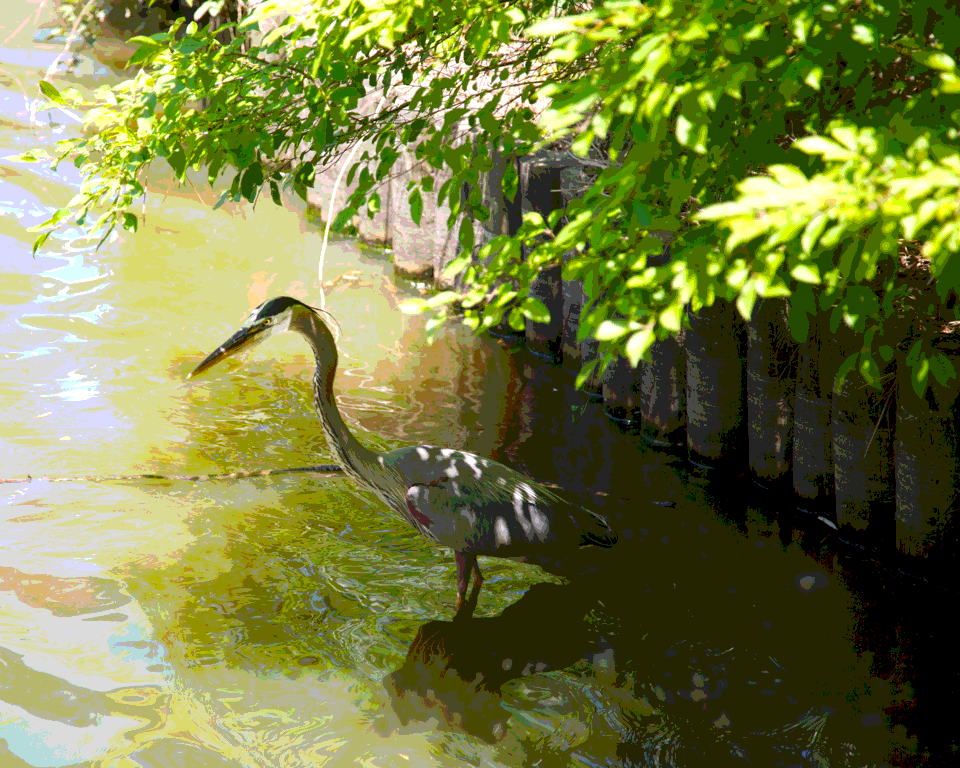
Next the following repeating generic pseudo-random noise texture (a poor grain proxy) is added in linear prior to quantization and conversion to sRGB.

This noise is very similar to the results of the “fract, sin/cos, dot” in-shader texture-free method described on Gregory Igehy’s Notes of Pseudo-Random Generator for Shaders. The resulting image after conversion.

While it is an improvement over quantization without grain, application of this grain results in various artifacts as the eye is distracted by the structure of the grain. Looking again at the noise texture, this time only one channel, it is possible to see a lot of low frequency content mixed in the noise.

To improve upon this, the noise can be shaped into a visually pleasing grain, for example by application of a high-pass filter on both the x and y axis. In this case a different cutoff frequency is used in each axis to leave a feeling of paper texture.

An alternative could be to start with some other photographic source converted into a tiling texture. Both of these cases can have problems caused by a non-even distribution of values in the grain texture. It is possible to re-shape the grain texture into a perfectly balanced distribution of values using the following method.

1. For all texels of a given channel build a 64-bit value: {32-bit channel intensity, 16-bit texel x coordinate, 16-bit texel y coordinate}.
2. Randomly shuttle the ordering of the 64-bit values (to deal with duplicates).
3. Use a radix sort to sort all the 64-bit values.
4. Take the sorted position divided by number of texels as the new texel channel intensity.
5. Use the packed {16-bit texel coordinates} to scatter the new texel intensity back to the original image.

Applying the above process to the prior grain texture yields the following result for a single channel.

And for the full color grain texture.

Application of this new grain to the original image yields the following high quality result (this is only a 3-bit per channel sRGB image).

Details on Grain Application

Starting with the technique used in the images in this post,

// Quantization steps, for 8-bit for example this would be 256.
float quantizationSteps;

// Linear color input.
float3 color = ...;

// This is used to limit the addition of grain around black to avoid increasing the black level.
// This should be a pre-computed constant.
// At zero, grain amplitude is limited such that the largest negative grain value would still quantize to zero.
// Showing the example for sRGB, the ConvertSrgbToLinear() does sRGB to linear conversion.
float grainBlackLimit = 0.5 * ConvertSrgbToLinear(1.0 / (quantizationSteps - 1.0));

// This should also be a pre-computed constant.
// With the exception of around the blacks, a constant linear amount of grain is added to the image.
// Technically with low amounts of quantization steps, it would also be good to limit around white as well.
// Given the primary usage case is high number of quantization steps,
// limiting around whites is not perceptually important.
// The largest linear distance between steps is always the highest output value.
// This sets the constant linear amount of grain to fully dither the highest output value.
// This does result in a higher-than-required amount of grain in the darks.
// Using 0.75 leaves overlap to ensure the grain does not disappear at the linear mid-point between steps.
float grainAmount = 0.75 * (ConvertSrgbToLinear(1.0 / (quantizationSteps - 1.0)) - 1.0);

// Point-sampled grain texture scaled to {-1.0 to 1.0}.
// Note the grain is sampled without a sRGB-to-linear conversion.
// Grain is a standard RGBA UNORM format (not sRGB labeled).
float3 grain = ...;

// Apply grain to linear color.
color = grain * min(color + grainBlackLimit, grainAmount) + color;

When grain is applied temporally, sending in a per-frame offset to SV_Position can be used to temporally offset the grain texture. A {2,3} Halton Sequence with a 1024 frame period works quite well. This method of adding grain is quite fast, only requiring {1 TEX, and 13 VALU instructions} extra to implement.

// Example minimal shader (ideally grain would get folded into some other pass).
// Showing with the associated VALU opcodes used interleaved in comments.
cbuffer CB0 : register(b0) { int2 halton; float2 grainConst; };
Texture2D texColor;
Texture2D texGrain;
float3 main(float4 vpos : SV_Position) : SV_Target {
  // 2x V_CVT_I32_F32
  int3 pos = int3(vpos.xy, 0);
  float3 color = texColor.Load(pos).rgb;
  // 2x V_ADD_I32, 2x V_BFE_U32
  pos.xy = (pos.xy + halton) & 255;
  float3 grain = texGrain.Load(pos).rgb;
  // 3x V_ADD_F32, 3x V_MIN_F32, 3x V_MAC_F32
  return grain * min(color + grainConst.x, grainConst.y) + color;
}

Other posts in this series

GDC 2015

Links to AMD Presentations shown at GDC 2015

TressFX

The TressFX library is AMD’s hair/fur rendering and simulation technology. TressFX is designed to use the GPU to simulate and render high-quality, realistic hair and fur.

ShadowFX

ShadowFX library provides a scalable GCN-optimized solution for deferred shadow filtering. It supports uniform and contact hardening shadow (CHS) kernels.

GeometryFX

GeometryFX improves the rasterizer efficiency by culling triangles that do not contribute to the output in a pre-pass. This allows the full chip to be used to process geometry, and...