Post-multiplication, left-handed coordinate system

Originally posted:

Axis in matrix

[X-AxisY-AxisZ-AxisTranslate↓↓↓↓m11m12m13m14m21m22m23m24m31m32m33m34m41m42m43m44]\begin{array}{c} \begin{bmatrix} \color{red} \textrm{X-Axis} & \color{green} \textrm{Y-Axis} & \color{blue} \textrm{Z-Axis} & \textrm{Translate} \\ \color{red} \downarrow & \color{green} \downarrow & \color{blue} \downarrow & \downarrow \\ \color{red} \mathbf{m_{11}} & \color{green} \mathbf{m_{12}} & \color{blue} \mathbf{m_{13}} & \mathbf{m_{14}}\\ \color{red} \mathbf{m_{21}} & \color{green} \mathbf{m_{22}} & \color{blue} \mathbf{m_{23}} & \mathbf{m_{24}}\\ \color{red} \mathbf{m_{31}} & \color{green} \mathbf{m_{32}} & \color{blue} \mathbf{m_{33}} & \mathbf{m_{34}}\\ \color{gray} m_{41} & \color{gray} m_{42} & \color{gray} m_{43} & \color{gray} m_{44}\\ \end{bmatrix} \end{array}

Translation Transformation

[100Tx010Ty001Tz0001]\begin{bmatrix} 1 & 0 & 0 & T_x\\ 0 & 1 & 0 & T_y\\ 0 & 0 & 1 & T_z\\ 0 & 0 & 0 & 1\\ \end{bmatrix}

Scale Transformation

[Sx0000Sy0000Sz00001]\begin{bmatrix} S_x & 0 & 0 & 0\\ 0 & S_y & 0 & 0\\ 0 & 0 & S_z & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix}

Rotation Transformation

  • From Euler Angles
X - AxisY - AxisZ - Axis[10000cos⁡(θ)−sin⁡(θ)00sin⁡(θ)cos⁡(θ)00001][cos⁡(θ)0sin⁡(θ)00100−sin⁡(θ)0cos⁡(θ)00001][cos⁡(θ)−sin⁡(θ)00sin⁡(θ)cos⁡(θ)0000100001]\begin{array}{ccc} \textrm{X - Axis} & \textrm{Y - Axis} & \textrm{Z - Axis} \\ \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & \cos(\theta) & -\sin(\theta) & 0\\ 0 & \sin(\theta) & \cos(\theta) & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} \cos(\theta) & 0 & \sin(\theta) & 0\\ 0 & 1 & 0 & 0\\ -\sin(\theta) & 0 & \cos(\theta) & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} \cos(\theta) & -\sin(\theta) & 0 & 0\\ \sin(\theta) & \cos(\theta) & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{array}
  • From Quaternion

Quaternion defined Q:a+bi+cj+dk=(r,v⃗)=(Qw,Qx,Qy,Qz)Q : a + b\mathbf{i} + c\mathbf{j} + d\mathbf{k} = (r, \vec{v}) = (Q_w, Q_x, Q_y, Q_z)

[1−2(Qy2+Qz2)2(QxQy−QzQw)2(QxQz+QyQw)02(QxQy+QzQw)1−2(Qx2+Qz2)2(QyQz−QxQw)02(QxQz−QyQw)2(QyQz+QxQw)1−2(Qx2+Qy2)00001]\begin{bmatrix} 1 - 2(Q_y^2 + Q_z^2) & 2(Q_xQ_y - Q_zQ_w) & 2(Q_xQ_z + Q_yQ_w) & 0\\ 2(Q_xQ_y + Q_zQ_w) & 1 - 2(Q_x^2 + Q_z^2) & 2(Q_yQ_z - Q_xQ_w) & 0\\ 2(Q_xQ_z - Q_yQ_w) & 2(Q_yQ_z + Q_xQ_w) & 1 - 2(Q_x^2 + Q_y^2) & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix}
  • From Axis Angle

Axis angle defined U:cos⁡(θ)+sin⁡(θ)(u^x,u^y,u^z)U : \cos(\theta) + \sin(\theta)(\hat{u}_x, \hat{u}_y, \hat{u}_z)

where :∣∣u^∣∣=1: ||\hat{u}|| = 1

[(1−c)u^x2+c(1−c)u^xu^y−su^z(1−c)u^xu^z+su^y0(1−c)u^xu^y+su^z(1−c)u^y2+c(1−c)u^yu^z−su^x0(1−c)u^xu^z−su^y(1−c)u^yu^z+su^x(1−c)u^z2+c00001]\begin{bmatrix} (1-c)\hat{u}_x^2 + c & (1-c)\hat{u}_x\hat{u}_y - s\hat{u}_z & (1-c)\hat{u}_x\hat{u}_z + s\hat{u}_y & 0\\ (1-c)\hat{u}_x\hat{u}_y + s\hat{u}_z & (1-c)\hat{u}_y^2 + c & (1-c)\hat{u}_y\hat{u}_z - s\hat{u}_x & 0\\ (1-c)\hat{u}_x\hat{u}_z - s\hat{u}_y & (1-c)\hat{u}_y\hat{u}_z + s\hat{u}_x & (1-c)\hat{u}_z^2 + c & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix}

Reflection Transformation

  • Axis Plane symmetry
XY PlaneXZ PlaneYZ Plane[1000010000−100001][10000−10000100001][−1000010000100001]\begin{array}{ccc} \textrm{XY Plane} & \textrm{XZ Plane} & \textrm{YZ Plane} \\ \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} -1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{array}
  • Axial symmetry
X - AxisY - AxisZ - Axis[10000−10000−100001][−1000010000−100001][−10000−10000100001]\begin{array}{ccc} \textrm{X - Axis} & \textrm{Y - Axis} & \textrm{Z - Axis} \\ \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} -1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} -1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{array}
  • Central symmetry
[−10000−10000−100001]\begin{bmatrix} -1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix}
  • Generic plane symmetry

Plane defined P:ax+by+cz+d=0P : ax + by + cz + d = 0

[1−2a2−2ab−2ac−2ad−2ab1−2b2−2bc−2bd−2ac−2bc1−2c2−2cd0001]\begin{bmatrix} 1-2a^2 & -2ab & -2ac & -2ad\\ -2ab & 1-2b^2 & -2bc & -2bd\\ -2ac & -2bc & 1-2c^2 & -2cd\\ 0 & 0 & 0 & 1\\ \end{bmatrix}

Shear Transformation

X - AxisY - AxisZ - AxisGeneral[1000Hy100Hz0100001][1Hx0001000Hz100001][10Hx001Hy000100001][1HxyHxz0Hyx1Hyz0HzxHzy100001]\begin{array}{cccc} \textrm{X - Axis} & \textrm{Y - Axis} & \textrm{Z - Axis} & \textrm{General}\\ \begin{bmatrix} 1 & 0 & 0 & 0\\ H_y & 1 & 0 & 0\\ H_z & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} 1 & H_x & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & H_z & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} 1 & 0 & H_x & 0\\ 0 & 1 & H_y & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} 1 & H_x^y & H_x^z & 0\\ H_y^x & 1 & H_y^z & 0\\ H_z^x & H_z^y & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{array}

Planar Projections Transformation

Orthographic Transformation

ll - left coordinate of the orthographic frustum

rr - right coordinate of the orthographic frustum

bb - bottom coordinate of the orthographic frustum

tt - top coordinate of the orthographic frustum

nn - distance to the near plane of the orthographic frustum

ff - distance to the far plane of the orthographic frustum

ww - width of the near plane of the orthographic frustum

hh - height of the near plane of the orthographic frustum

  • Clip Space z∈[0,1]z \in \lbrack 0,1 \rbrack
View SpaceLeft-handed NDC SpaceRight-handed NDC Space
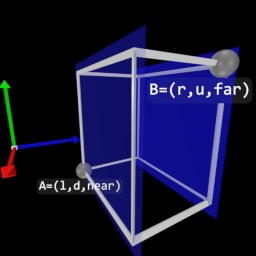imageimageimageimage
GeneralSymmetricSymmetric 2D[2r−l00r+lr−l02t−b0t+bt−b001f−n−nf−n0001][2w00002h00001f−n−nf−n0001][2w00002h000012120001]\begin{array}{ccc} \textrm{General} & \textrm{Symmetric} & \textrm{Symmetric 2D} \\ \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & \frac{r+l}{r-l}\\ 0 & \frac{2}{t-b} & 0 & \frac{t+b}{t-b}\\ 0 & 0 & \frac{1}{f-n} & -\frac{n}{f-n}\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} \frac{2}{w} & 0 & 0 & 0\\ 0 & \frac{2}{h} & 0 & 0\\ 0 & 0 & \frac{1}{f-n} & -\frac{n}{f-n}\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} \frac{2}{w} & 0 & 0 & 0\\ 0 & \frac{2}{h} & 0 & 0\\ 0 & 0 & \frac{1}{2} & \frac{1}{2}\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{array}
  • Clip Space z∈[−1,1]z \in \lbrack -1,1 \rbrack
View SpaceLeft-handed NDC SpaceRight-handed NDC Space
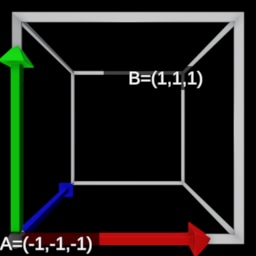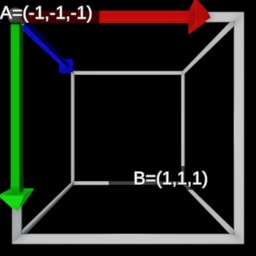imageimageimageimage
GeneralSymmetricSymmetric 2D[2r−l00r+lr−l02t−b0t+bt−b002f−n−f+nf−n0001][2w00002h00002f−n−f+nf−n0001][1w00001h0000100001]\begin{array}{ccc} \textrm{General} & \textrm{Symmetric} & \textrm{Symmetric 2D} \\ \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & \frac{r+l}{r-l}\\ 0 & \frac{2}{t-b} & 0 & \frac{t+b}{t-b}\\ 0 & 0 & \frac{2}{f-n} & -\frac{f+n}{f-n}\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} \frac{2}{w} & 0 & 0 & 0\\ 0 & \frac{2}{h} & 0 & 0\\ 0 & 0 & \frac{2}{f-n} & -\frac{f+n}{f-n}\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} \frac{1}{w} & 0 & 0 & 0\\ 0 & \frac{1}{h} & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{array}

Perspective Transformation

ll - left coordinate of the perspective frustum

rr - right coordinate of the perspective frustum

bb - bottom coordinate of the perspective frustum

tt - top coordinate of the perspective frustum

nn - distance to the near plane of the perspective frustum

ff - distance to the far plane of the perspective frustum

ww - width of the near plane of the perspective frustum

hh - height of the near plane of the perspective frustum

α\alpha - angle between of left and right frustum planes of the perspective frustum

β\beta - angle between of top and bottom frustum planes of the perspective frustum

  • Perspective Transformation [n,f]\mathbf{\lbrack n,f \rbrack}, Clip Space z∈[0,1]\mathbf{z \in \lbrack 0,1 \rbrack}
View SpaceLeft-handed NDC SpaceRight-handed NDC Space
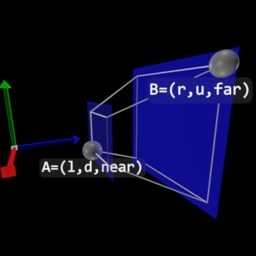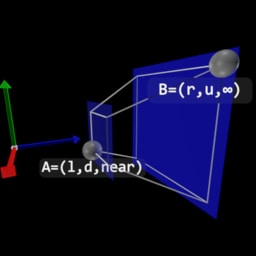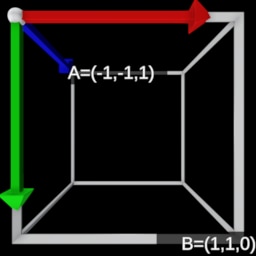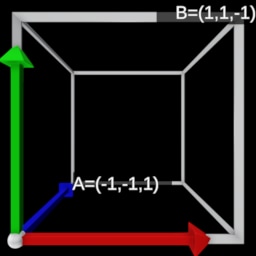imageimageimageimage
FrustumSymmetric α,βSymmetric w,h[2nr−l0−r+lr−l002nt−b−t+bt−b000ff−n−fnf−n0010][whcot⁡(α2)0000cot⁡(α2)0000ff−n−fnf−n0010][cot⁡(β2)0000hwcot⁡(β2)0000ff−n−fnf−n0010]\begin{array}{ccc} \textrm{Frustum} & \textrm{Symmetric } \alpha,\beta & \textrm{Symmetric } w,h\\ \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0\\ 0 & 0 & \frac{f}{f-n} & -\frac{fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \frac{w}{h}\cot(\frac{\alpha}{2}) & 0 & 0 & 0\\ 0 & \cot(\frac{\alpha}{2}) & 0 & 0\\ 0 & 0 & \frac{f}{f-n} & -\frac{fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \cot(\frac{\beta}{2}) & 0 & 0 & 0\\ 0 & \frac{h}{w}\cot(\frac{\beta}{2}) & 0 & 0\\ 0 & 0 & \frac{f}{f-n} & -\frac{fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \end{array}
  • Perspective Transformation infinite far plane [n,∞]\mathbf{\lbrack n,\infty \rbrack}, Clip Space z∈[0,1]\mathbf{z \in \lbrack 0,1 \rbrack}
View SpaceLeft-handed NDC SpaceRight-handed NDC Space
imageimageimageimage
FrustumSymmetric α,βSymmetric w,h[2nr−l0−r+lr−l002nt−b−t+bt−b0001−n0010][whcot⁡(α2)0000cot⁡(α2)00001−n0010][cot⁡(β2)0000hwcot⁡(β2)00001−n0010]\begin{array}{ccc} \textrm{Frustum} & \textrm{Symmetric } \alpha,\beta & \textrm{Symmetric } w,h\\ \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0\\ 0 & 0 & 1 & -n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \frac{w}{h}\cot(\frac{\alpha}{2}) & 0 & 0 & 0\\ 0 & \cot(\frac{\alpha}{2}) & 0 & 0\\ 0 & 0 & 1 & -n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \cot(\frac{\beta}{2}) & 0 & 0 & 0\\ 0 & \frac{h}{w}\cot(\frac{\beta}{2}) & 0 & 0\\ 0 & 0 & 1 & -n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \end{array}
  • Perspective Transformation [n,f]\mathbf{\lbrack n,f \rbrack}, Reversed Clip Space z∈[1,0]\mathbf{z \in \lbrack 1,0 \rbrack}
View SpaceLeft-handed NDC SpaceRight-handed NDC Space
imageimageimageimage
FrustumSymmetric α,βSymmetric w,h[2nr−l0−r+lr−l002nt−b−t+bt−b000−nf−nfnf−n0010][whcot⁡(α2)0000cot⁡(α2)0000−nf−nfnf−n0010][cot⁡(β2)0000hwcot⁡(β2)0000−nf−nfnf−n0010]\begin{array}{ccc} \textrm{Frustum} & \textrm{Symmetric } \alpha,\beta & \textrm{Symmetric } w,h\\ \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0\\ 0 & 0 & -\frac{n}{f-n} & \frac{fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \frac{w}{h}\cot(\frac{\alpha}{2}) & 0 & 0 & 0\\ 0 & \cot(\frac{\alpha}{2}) & 0 & 0\\ 0 & 0 & -\frac{n}{f-n} & \frac{fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \cot(\frac{\beta}{2}) & 0 & 0 & 0\\ 0 & \frac{h}{w}\cot(\frac{\beta}{2}) & 0 & 0\\ 0 & 0 & -\frac{n}{f-n} & \frac{fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \end{array}
  • Perspective Transformation infinite far plane [n,∞]\mathbf{\lbrack n,\infty \rbrack}, Reversed Clip Space z∈[1,0]\mathbf{z \in \lbrack 1,0 \rbrack}
View SpaceLeft-handed NDC SpaceRight-handed NDC Space
imageimageimageimage
FrustumSymmetric α,βSymmetric w,h[2nr−l0−r+lr−l002nt−b−t+bt−b0000n0010][whcot⁡(α2)0000cot⁡(α2)00000n0010][cot⁡(β2)0000hwcot⁡(β2)00000n0010]\begin{array}{ccc} \textrm{Frustum} & \textrm{Symmetric } \alpha,\beta & \textrm{Symmetric } w,h\\ \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0\\ 0 & 0 & 0 & n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \frac{w}{h}\cot(\frac{\alpha}{2}) & 0 & 0 & 0\\ 0 & \cot(\frac{\alpha}{2}) & 0 & 0\\ 0 & 0 & 0 & n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \cot(\frac{\beta}{2}) & 0 & 0 & 0\\ 0 & \frac{h}{w}\cot(\frac{\beta}{2}) & 0 & 0\\ 0 & 0 & 0 & n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \end{array}
  • Perspective Transformation [n,f]\mathbf{\lbrack n,f \rbrack}, Clip Space z∈[−1,1]\mathbf{z \in \lbrack -1,1 \rbrack}
View SpaceLeft-handed NDC SpaceRight-handed NDC Space
imageimageimageimage
FrustumSymmetric α,βSymmetric w,h[2nr−l0−r+lr−l002nt−b−t+bt−b000f+nf−n−2fnf−n0010][whcot⁡(α2)0000cot⁡(α2)0000f+nf−n−2fnf−n0010][cot⁡(β2)0000hwcot⁡(β2)0000f+nf−n−2fnf−n0010]\begin{array}{ccc} \textrm{Frustum} & \textrm{Symmetric } \alpha,\beta & \textrm{Symmetric } w,h\\ \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0\\ 0 & 0 & \frac{f+n}{f-n} & -\frac{2fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \frac{w}{h}\cot(\frac{\alpha}{2}) & 0 & 0 & 0\\ 0 & \cot(\frac{\alpha}{2}) & 0 & 0\\ 0 & 0 & \frac{f+n}{f-n} & -\frac{2fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \cot(\frac{\beta}{2}) & 0 & 0 & 0\\ 0 & \frac{h}{w}\cot(\frac{\beta}{2}) & 0 & 0\\ 0 & 0 & \frac{f+n}{f-n} & -\frac{2fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \end{array}
  • Perspective Transformation infinite far plane [n,∞]\mathbf{\lbrack n,\infty \rbrack}, Clip Space z∈[−1,1]\mathbf{z \in \lbrack -1,1 \rbrack}
View SpaceLeft-handed NDC SpaceRight-handed NDC Space
imageimageimageimage
FrustumSymmetric α,βSymmetric w,h[2nr−l0−r+lr−l002nt−b−t+bt−b0001−2n0010][whcot⁡(α2)0000cot⁡(α2)00001−2n0010][cot⁡(β2)0000hwcot⁡(β2)00001−2n0010]\begin{array}{ccc} \textrm{Frustum} & \textrm{Symmetric } \alpha,\beta & \textrm{Symmetric } w,h\\ \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0\\ 0 & 0 & 1 & -2n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \frac{w}{h}\cot(\frac{\alpha}{2}) & 0 & 0 & 0\\ 0 & \cot(\frac{\alpha}{2}) & 0 & 0\\ 0 & 0 & 1 & -2n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \cot(\frac{\beta}{2}) & 0 & 0 & 0\\ 0 & \frac{h}{w}\cot(\frac{\beta}{2}) & 0 & 0\\ 0 & 0 & 1 & -2n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \end{array}
  • Perspective Transformation [n,f]\mathbf{\lbrack n,f \rbrack}, Reversed Clip Space z∈[1,−1]\mathbf{z \in \lbrack 1,-1 \rbrack}
View SpaceLeft-handed NDC SpaceRight-handed NDC Space
imageimageimageimage
FrustumSymmetric α,βSymmetric w,h[2nr−l0−r+lr−l002nt−b−t+bt−b000−f+nf−n2fnf−n0010][whcot⁡(α2)0000cot⁡(α2)0000−f+nf−n2fnf−n0010][cot⁡(β2)0000hwcot⁡(β2)0000−f+nf−n2fnf−n0010]\begin{array}{ccc} \textrm{Frustum} & \textrm{Symmetric } \alpha,\beta & \textrm{Symmetric } w,h\\ \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0\\ 0 & 0 & -\frac{f+n}{f-n} & \frac{2fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \frac{w}{h}\cot(\frac{\alpha}{2}) & 0 & 0 & 0\\ 0 & \cot(\frac{\alpha}{2}) & 0 & 0\\ 0 & 0 & -\frac{f+n}{f-n} & \frac{2fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \cot(\frac{\beta}{2}) & 0 & 0 & 0\\ 0 & \frac{h}{w}\cot(\frac{\beta}{2}) & 0 & 0\\ 0 & 0 & -\frac{f+n}{f-n} & \frac{2fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \end{array}
  • Perspective Transformation infinite far plane [n,∞]\mathbf{\lbrack n,\infty \rbrack}, Reversed Clip Space z∈[1,−1]\mathbf{z \in \lbrack 1,-1 \rbrack}
View SpaceLeft-handed NDC SpaceRight-handed NDC Space
imageimageimageimage
FrustumSymmetric α,βSymmetric w,h[2nr−l0−r+lr−l002nt−b−t+bt−b000−12n0010][whcot⁡(α2)0000cot⁡(α2)0000−11002n0][cot⁡(β2)0000hwcot⁡(β2)0000−12n0010]\begin{array}{ccc} \textrm{Frustum} & \textrm{Symmetric } \alpha,\beta & \textrm{Symmetric } w,h\\ \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0\\ 0 & 0 & -1 & 2n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \frac{w}{h}\cot(\frac{\alpha}{2}) & 0 & 0 & 0\\ 0 & \cot(\frac{\alpha}{2}) & 0 & 0\\ 0 & 0 & -1 & 1\\ 0 & 0 & 2n & 0\\ \end{bmatrix} & \begin{bmatrix} \cot(\frac{\beta}{2}) & 0 & 0 & 0\\ 0 & \frac{h}{w}\cot(\frac{\beta}{2}) & 0 & 0\\ 0 & 0 & -1 & 2n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \end{array}

Jitter Orthographic Transformation

ll - left coordinate of the orthographic frustum

rr - right coordinate of the orthographic frustum

bb - bottom coordinate of the orthographic frustum

tt - top coordinate of the orthographic frustum

nn - distance to the near plane of the orthographic frustum

ff - distance to the far plane of the orthographic frustum

ww - width of the near plane of the orthographic frustum

hh - height of the near plane of the orthographic frustum

jxj_x - jitter in NDC space in the x-direction

jyj_y - jitter in NDC space in the y-direction

  • Jitter Orthographic Transformation Clip Space z∈[0,1]z \in \lbrack 0,1 \rbrack
GeneralSymmetricSymmetric 2D[2r−l00r(1+jx)+l(1−jx)r−l02t−b0t(1+jy)+b(1−jy)t−b001f−n−nf−n0001][2w00jx02h0jy001f−n−nf−n0001][2w00jx02h0jy0012120001]\begin{array}{ccc} \textrm{General} & \textrm{Symmetric} & \textrm{Symmetric 2D} \\ \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & \frac{r(1+j_x)+l(1-j_x)}{r-l}\\ 0 & \frac{2}{t-b} & 0 & \frac{t(1+j_y)+b(1-j_y)}{t-b}\\ 0 & 0 & \frac{1}{f-n} & -\frac{n}{f-n}\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} \frac{2}{w} & 0 & 0 & j_x\\ 0 & \frac{2}{h} & 0 & j_y\\ 0 & 0 & \frac{1}{f-n} & -\frac{n}{f-n}\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} \frac{2}{w} & 0 & 0 & j_x\\ 0 & \frac{2}{h} & 0 & j_y\\ 0 & 0 & \frac{1}{2} & \frac{1}{2}\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{array}
  • Jitter Orthographic Transformation Clip Space z∈[−1,1]z \in \lbrack -1,1 \rbrack
GeneralSymmetricSymmetric 2D[2r−l00r(1+jx)+l(1−jx)r−l02t−b0t(1+jy)+b(1−jy)t−b002f−n−f+nf−n0001][2w00jx02h0jy002f−n−f+nf−n0001][1w00jx01h0jy00100001]\begin{array}{ccc} \textrm{General} & \textrm{Symmetric} & \textrm{Symmetric 2D} \\ \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & \frac{r(1+j_x)+l(1-j_x)}{r-l}\\ 0 & \frac{2}{t-b} & 0 & \frac{t(1+j_y)+b(1-j_y)}{t-b}\\ 0 & 0 & \frac{2}{f-n} & -\frac{f+n}{f-n}\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} \frac{2}{w} & 0 & 0 & j_x\\ 0 & \frac{2}{h} & 0 & j_y\\ 0 & 0 & \frac{2}{f-n} & -\frac{f+n}{f-n}\\ 0 & 0 & 0 & 1\\ \end{bmatrix} & \begin{bmatrix} \frac{1}{w} & 0 & 0 & j_x\\ 0 & \frac{1}{h} & 0 & j_y\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{array}

Jitter Perspective Transformation

ll - left coordinate of the perspective frustum

rr - right coordinate of the perspective frustum

bb - bottom coordinate of the perspective frustum

tt - top coordinate of the perspective frustum

nn - distance to the near plane of the perspective frustum

ff - distance to the far plane of the perspective frustum

ww - width of the near plane of the perspective frustum

hh - height of the near plane of the perspective frustum

jxj_x - jitter in NDC space in the x-direction

jyj_y - jitter in NDC space in the y-direction

α\alpha - angle between of left and right frustum planes of the perspective frustum

β\beta - angle between of top and bottom frustum planes of the perspective frustum

  • Jitter Perspective Transformation [n,f]\mathbf{\lbrack n,f \rbrack}, Clip Space z∈[0,1]\mathbf{z \in \lbrack 0,1 \rbrack}
FrustumSymmetric α,βSymmetric w,h[2nr−l0−r(1+jx)+l(1−jx)r−l002nt−b−t(1+jy)+b(1−jy)t−b000ff−n−fnf−n0010][whcot⁡(α2)0−jx00cot⁡(α2)−jy000ff−n−fnf−n0010][cot⁡(β2)0−jx00hwcot⁡(β2)−jy000ff−n−fnf−n0010]\begin{array}{ccc} \textrm{Frustum} & \textrm{Symmetric } \alpha,\beta & \textrm{Symmetric } w,h\\ \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r(1+j_x)+l(1-j_x)}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t(1+j_y)+b(1-j_y)}{t-b} & 0\\ 0 & 0 & \frac{f}{f-n} & -\frac{fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \frac{w}{h}\cot(\frac{\alpha}{2}) & 0 & -j_x & 0\\ 0 & \cot(\frac{\alpha}{2}) & -j_y & 0\\ 0 & 0 & \frac{f}{f-n} & -\frac{fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \cot(\frac{\beta}{2}) & 0 & -j_x & 0\\ 0 & \frac{h}{w}\cot(\frac{\beta}{2}) & -j_y & 0\\ 0 & 0 & \frac{f}{f-n} & -\frac{fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \end{array}
  • Jitter Perspective Transformation infinite far plane [n,∞]\mathbf{\lbrack n,\infty \rbrack}, Clip Space z∈[0,1]\mathbf{z \in \lbrack 0,1 \rbrack}
FrustumSymmetric α,βSymmetric w,h[2nr−l0−r(1+jx)+l(1−jx)r−l002nt−b−t(1+jy)+b(1−jy)t−b0001−n0010][whcot⁡(α2)0−jx00cot⁡(α2)−jy0001−n0010][cot⁡(β2)0−jx00hwcot⁡(β2)−jy0001−n0010]\begin{array}{ccc} \textrm{Frustum} & \textrm{Symmetric } \alpha,\beta & \textrm{Symmetric } w,h\\ \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r(1+j_x)+l(1-j_x)}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t(1+j_y)+b(1-j_y)}{t-b} & 0\\ 0 & 0 & 1 & -n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \frac{w}{h}\cot(\frac{\alpha}{2}) & 0 & -j_x & 0\\ 0 & \cot(\frac{\alpha}{2}) & -j_y & 0\\ 0 & 0 & 1 & -n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \cot(\frac{\beta}{2}) & 0 & -j_x & 0\\ 0 & \frac{h}{w}\cot(\frac{\beta}{2}) & -j_y & 0\\ 0 & 0 & 1 & -n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \end{array}
  • Jitter Perspective Transformation [n,f]\mathbf{\lbrack n,f \rbrack}, Reversed Clip Space z∈[1,0]\mathbf{z \in \lbrack 1,0 \rbrack}
FrustumSymmetric α,βSymmetric w,h[2nr−l0−r(1+jx)+l(1−jx)r−l002nt−b−t(1+jy)+b(1−jy)t−b000−nf−nfnf−n0010][whcot⁡(α2)0−jx00cot⁡(α2)−jy000−nf−nfnf−n0010][cot⁡(β2)0−jx00hwcot⁡(β2)−jy000−nf−nfnf−n0010]\begin{array}{ccc} \textrm{Frustum} & \textrm{Symmetric } \alpha,\beta & \textrm{Symmetric } w,h\\ \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r(1+j_x)+l(1-j_x)}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t(1+j_y)+b(1-j_y)}{t-b} & 0\\ 0 & 0 & -\frac{n}{f-n} & \frac{fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \frac{w}{h}\cot(\frac{\alpha}{2}) & 0 & -j_x & 0\\ 0 & \cot(\frac{\alpha}{2}) & -j_y & 0\\ 0 & 0 & -\frac{n}{f-n} & \frac{fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \cot(\frac{\beta}{2}) & 0 & -j_x & 0\\ 0 & \frac{h}{w}\cot(\frac{\beta}{2}) & -j_y & 0\\ 0 & 0 & -\frac{n}{f-n} & \frac{fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \end{array}
  • Jitter Perspective Transformation infinite far plane [n,∞]\mathbf{\lbrack n,\infty \rbrack}, Reversed Clip Space z∈[1,0]\mathbf{z \in \lbrack 1,0 \rbrack}
FrustumSymmetric α,βSymmetric w,h[2nr−l0−r(1+jx)+l(1−jx)r−l002nt−b−t(1+jy)+b(1−jy)t−b0000n0010][whcot⁡(α2)0−jx00cot⁡(α2)−jy0000n0010][cot⁡(β2)0−jx00hwcot⁡(β2)−jy0000n0010]\begin{array}{ccc} \textrm{Frustum} & \textrm{Symmetric } \alpha,\beta & \textrm{Symmetric } w,h\\ \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r(1+j_x)+l(1-j_x)}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t(1+j_y)+b(1-j_y)}{t-b} & 0\\ 0 & 0 & 0 & n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \frac{w}{h}\cot(\frac{\alpha}{2}) & 0 & -j_x & 0\\ 0 & \cot(\frac{\alpha}{2}) & -j_y & 0\\ 0 & 0 & 0 & n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \cot(\frac{\beta}{2}) & 0 & -j_x & 0\\ 0 & \frac{h}{w}\cot(\frac{\beta}{2}) & -j_y & 0\\ 0 & 0 & 0 & n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \end{array}
  • Jitter Perspective Transformation [n,f]\mathbf{\lbrack n,f \rbrack}, Clip Space z∈[−1,1]\mathbf{z \in \lbrack -1,1 \rbrack}
FrustumSymmetric α,βSymmetric w,h[2nr−l0−r(1+jx)+l(1−jx)r−l002nt−b−t(1+jy)+b(1−jy)t−b000f+nf−n−2fnf−n0010][whcot⁡(α2)0−jx00cot⁡(α2)−jy000f+nf−n−2fnf−n0010][cot⁡(β2)0−jx00hwcot⁡(β2)−jy000f+nf−n−2fnf−n0010]\begin{array}{ccc} \textrm{Frustum} & \textrm{Symmetric } \alpha,\beta & \textrm{Symmetric } w,h\\ \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r(1+j_x)+l(1-j_x)}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t(1+j_y)+b(1-j_y)}{t-b} & 0\\ 0 & 0 & \frac{f+n}{f-n} & -\frac{2fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \frac{w}{h}\cot(\frac{\alpha}{2}) & 0 & -j_x & 0\\ 0 & \cot(\frac{\alpha}{2}) & -j_y & 0\\ 0 & 0 & \frac{f+n}{f-n} & -\frac{2fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \cot(\frac{\beta}{2}) & 0 & -j_x & 0\\ 0 & \frac{h}{w}\cot(\frac{\beta}{2}) & -j_y & 0\\ 0 & 0 & \frac{f+n}{f-n} & -\frac{2fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \end{array}
  • Jitter Perspective Transformation infinite far plane [n,∞]\mathbf{\lbrack n,\infty \rbrack}, Clip Space z∈[−1,1]\mathbf{z \in \lbrack -1,1 \rbrack}
FrustumSymmetric α,βSymmetric w,h[2nr−l0−r(1+jx)+l(1−jx)r−l002nt−b−t(1+jy)+b(1−jy)t−b0001−2n0010][whcot⁡(α2)0−jx00cot⁡(α2)−jy0001−2n0010][cot⁡(β2)0−jx00hwcot⁡(β2)−jy0001−2n0010]\begin{array}{ccc} \textrm{Frustum} & \textrm{Symmetric } \alpha,\beta & \textrm{Symmetric } w,h\\ \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r(1+j_x)+l(1-j_x)}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t(1+j_y)+b(1-j_y)}{t-b} & 0\\ 0 & 0 & 1 & -2n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \frac{w}{h}\cot(\frac{\alpha}{2}) & 0 & -j_x & 0\\ 0 & \cot(\frac{\alpha}{2}) & -j_y & 0\\ 0 & 0 & 1 & -2n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \cot(\frac{\beta}{2}) & 0 & -j_x & 0\\ 0 & \frac{h}{w}\cot(\frac{\beta}{2}) & -j_y & 0\\ 0 & 0 & 1 & -2n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \end{array}
  • Jitter Perspective Transformation [n,f]\mathbf{\lbrack n,f \rbrack}, Reversed Clip Space z∈[1,−1]\mathbf{z \in \lbrack 1,-1 \rbrack}
FrustumSymmetric α,βSymmetric w,h[2nr−l0−r(1+jx)+l(1−jx)r−l002nt−b−t(1+jy)+b(1−jy)t−b000−f+nf−n2fnf−n0010][whcot⁡(α2)0−jx00cot⁡(α2)−jy000−f+nf−n2fnf−n0010][cot⁡(β2)0−jx00hwcot⁡(β2)−jy000−f+nf−n2fnf−n0010]\begin{array}{ccc} \textrm{Frustum} & \textrm{Symmetric } \alpha,\beta & \textrm{Symmetric } w,h\\ \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r(1+j_x)+l(1-j_x)}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t(1+j_y)+b(1-j_y)}{t-b} & 0\\ 0 & 0 & -\frac{f+n}{f-n} & \frac{2fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \frac{w}{h}\cot(\frac{\alpha}{2}) & 0 & -j_x & 0\\ 0 & \cot(\frac{\alpha}{2}) & -j_y & 0\\ 0 & 0 & -\frac{f+n}{f-n} & \frac{2fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \cot(\frac{\beta}{2}) & 0 & -j_x & 0\\ 0 & \frac{h}{w}\cot(\frac{\beta}{2}) & -j_y & 0\\ 0 & 0 & -\frac{f+n}{f-n} & \frac{2fn}{f-n}\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \end{array}
  • Jitter Perspective Transformation infinite far plane [n,∞]\mathbf{\lbrack n,\infty \rbrack}, Reversed Clip Space z∈[1,−1]\mathbf{z \in \lbrack 1,-1 \rbrack}
FrustumSymmetric α,βSymmetric w,h[2nr−l0−r(1+jx)+l(1−jx)r−l002nt−b−t(1+jy)+b(1−jy)t−b000−12n0010][whcot⁡(α2)0−jx00cot⁡(α2)−jy000−11002n0][cot⁡(β2)0−jx00hwcot⁡(β2)−jy000−12n0010]\begin{array}{ccc} \textrm{Frustum} & \textrm{Symmetric } \alpha,\beta & \textrm{Symmetric } w,h\\ \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r(1+j_x)+l(1-j_x)}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t(1+j_y)+b(1-j_y)}{t-b} & 0\\ 0 & 0 & -1 & 2n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} & \begin{bmatrix} \frac{w}{h}\cot(\frac{\alpha}{2}) & 0 & -j_x & 0\\ 0 & \cot(\frac{\alpha}{2}) & -j_y & 0\\ 0 & 0 & -1 & 1\\ 0 & 0 & 2n & 0\\ \end{bmatrix} & \begin{bmatrix} \cot(\frac{\beta}{2}) & 0 & -j_x & 0\\ 0 & \frac{h}{w}\cot(\frac{\beta}{2}) & -j_y & 0\\ 0 & 0 & -1 & 2n\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \end{array}

Camera Transformations

  • “Look At” Transformation

at - position of the point at which the camera will be pointing at

eye - position of the camera

up - “Up” direction of the camera

C⃗\vec{C} - “Forward” vector

A⃗\vec{A} - “Right” vector

B⃗\vec{B} - “Up” vector

C⃗=at⃗−eye⃗∥at⃗−eye⃗∥\vec{C} = \frac{\vec{\textrm{at}} - \vec{\textrm{eye}}}{\|\vec{\textrm{at}} - \vec{\textrm{eye}}\|} A⃗=up⃗×C⃗\vec{A} = \vec{\textrm{up}} \times \vec{C} B⃗=C⃗×A⃗\vec{B} = \vec{C} \times \vec{A}

[A⃗xB⃗xC⃗x−(A⃗⋅eye⃗)A⃗yB⃗yC⃗y−(B⃗⋅eye⃗)A⃗zB⃗zC⃗z−(C⃗⋅eye⃗)0001]\begin{bmatrix} \vec{A}_x & \vec{B}_x & \vec{C}_x & -(\vec{A} \cdot \vec{\textrm{eye}})\\ \vec{A}_y & \vec{B}_y & \vec{C}_y & -(\vec{B} \cdot \vec{\textrm{eye}})\\ \vec{A}_z & \vec{B}_z & \vec{C}_z & -(\vec{C} \cdot \vec{\textrm{eye}})\\ 0 & 0 & 0 & 1\\ \end{bmatrix}
  • “Look To” Transformation

dir - desired direction of the camera

up - “Up” direction of the camera

C⃗\vec{C} - “Forward” vector

A⃗\vec{A} - “Right” vector

B⃗\vec{B} - “Up” vector

C⃗=dir⃗\vec{C} = \vec{\textrm{dir}} A⃗=up⃗×C⃗\vec{A} = \vec{\textrm{up}} \times \vec{C} B⃗=C⃗×A⃗\vec{B} = \vec{C} \times \vec{A}

[A⃗xB⃗xC⃗x−(A⃗⋅eye⃗)A⃗yB⃗yC⃗y−(B⃗⋅eye⃗)A⃗zB⃗zC⃗z−(C⃗⋅eye⃗)0001]\begin{bmatrix} \vec{A}_x & \vec{B}_x & \vec{C}_x & -(\vec{A} \cdot \vec{\textrm{eye}})\\ \vec{A}_y & \vec{B}_y & \vec{C}_y & -(\vec{B} \cdot \vec{\textrm{eye}})\\ \vec{A}_z & \vec{B}_z & \vec{C}_z & -(\vec{C} \cdot \vec{\textrm{eye}})\\ 0 & 0 & 0 & 1\\ \end{bmatrix}

Miscellaneous Matrices

  • Planar Shadow Projection

Plane defined P:Ax+By+Cz+D=0P: Ax + By + Cz + D = 0

Light position L:(Lx,Ly,Lz)L: (L_x, L_y, L_z)

where w=0w = 0 for direction light

w=1w = 1 for point light

L⃗=(Lx,Ly,Lx,w)\vec{L} = (L_x, L_y, L_x, w) P⃗=(A,B,C,D)\vec{P} = (A, B, C, D) k=P⃗⋅L⃗k = \vec{P} \cdot \vec{L}

[k−P⃗xL⃗x−P⃗xL⃗y−P⃗xL⃗z−P⃗xL⃗w−P⃗yL⃗xk−P⃗yL⃗y−P⃗yL⃗z−P⃗yL⃗w−P⃗zL⃗x−P⃗zL⃗yk−P⃗zL⃗z−P⃗zL⃗w−P⃗wL⃗x−P⃗wL⃗y−P⃗wL⃗zk−P⃗wL⃗w]\begin{bmatrix} k - \vec{P}_x \vec{L}_x & -\vec{P}_x \vec{L}_y & -\vec{P}_x \vec{L}_z & -\vec{P}_x \vec{L}_w \\ -\vec{P}_y \vec{L}_x & k - \vec{P}_y \vec{L}_y & -\vec{P}_y \vec{L}_z & -\vec{P}_y \vec{L}_w \\ -\vec{P}_z \vec{L}_x & -\vec{P}_z \vec{L}_y & k - \vec{P}_z \vec{L}_z & -\vec{P}_z \vec{L}_w \\ -\vec{P}_w \vec{L}_x & -\vec{P}_w \vec{L}_y & -\vec{P}_w \vec{L}_z & k - \vec{P}_w \vec{L}_w \\ \end{bmatrix}

Related software

Related news and technical articles

Related videos