Welcome to our guest posting from Sebastian Aaltonen, co-founder of Second Order LTD and previously senior rendering lead at Ubisoft®. Second Order have recently announced their first game, Claybook! Alongside the game looking like really great fun, its renderer is novel, using the GPU in very non-traditional ways in order to achieve its look. Check out Claybook!
Sebastian is going to cover an interesting problem he faced while working on Claybook: how you can optimize GPU occupancy and resource usage of compute shaders that use large thread groups.
Occupancy and Resource Usage Optimization with Large Thread Groups
When using a compute shader, it is important to consider the impact of thread group size on performance. Limited register space, memory latency and SIMD occupancy each affect shader performance in different ways. This article discusses potential performance issues, and techniques and optimizations that can dramatically increase performance if correctly applied. This article will be focusing on the problem set of large thread groups, but these tips and tricks are helpful in the common case as well.
Background
The DirectX® 11 Shader Model 5 compute shader specification (2009) mandates a maximum allowable memory size per thread group of 32 KiB, and a maximum workgroup size of 1024 threads. There is no specified maximum register count, and the compiler can spill registers to memory if necessitated by register pressure. However, due to memory latency, spilling entails a significant negative performance impact and should be avoided in production code.
Modern AMD GPUs are able to execute two groups of 1024 threads simultaneously on a single compute unit (CU). However, in order to maximize occupancy, shaders must minimize register and LDS usage so that resources required by all threads will fit within the CU.
AMD GCN compute unit (CU)
Consider the architecture of a GCN compute unit:
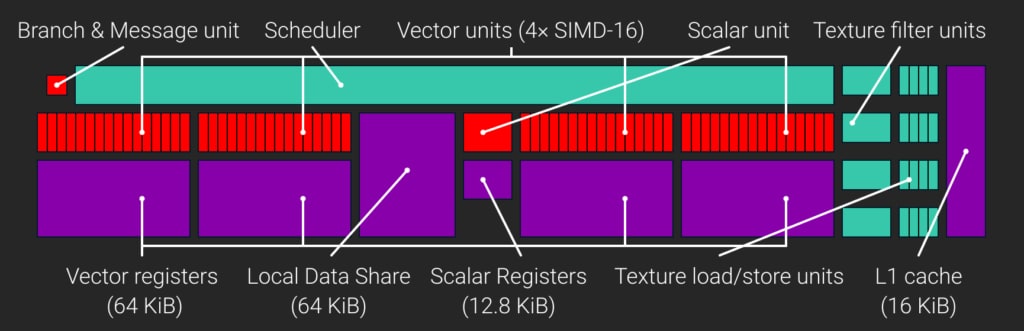
A GCN CU includes four SIMDs, each with a 64 KiB register file of 32-bit VGPRs (Vector General-Purpose Registers), for a total of 65,536 VGPRs per CU. Every CU also has a register file of 32-bit SGPRs (scalar general-purpose registers). Until GCN3, each CU contained 512 SGPRs, and from GCN3 on the count was bumped to 800. That yields 3200 SGPRs total per CU, or 12.5 KiB.
The smallest unit of scheduled work for the CU to run is called a wave, and each wave contains 64 threads. Each of the four SIMDs in the CU can schedule up to 10 concurrent waves. The CU may suspend a wave, and execute another wave, while waiting for memory operations to complete. This helps to hide latency and maximize use of the CU’s compute resources.
The size of the SIMD VGPR files introduce an important limit: VGPRs of the SIMD are evenly divided between threads of the active waves. If a shader requires more VGPRs than are available, the SIMD will not be able to execute the optimal number of waves. Occupancy, a measure of the parallel work that the GPU could perform at a given time, will suffer as a result.
Each GCN CU has 64 KiB Local Data Share (LDS). LDS is used to store the groupshared data of compute shader thread groups. Direct3D limits the amount of groupshared data a single thread group can use to 32 KiB. Thus we need to run at least two groups on each CU to fully utilize the LDS.
Large thread group resource goals
My example shader in this article is a complex GPGPU physics solver with thread group size of 1024. This shader uses maximum group size and maximum amount of groupshared memory. It benefits from a large group size, because it solves physics constraints using groupshared memory as temporal storage between multiple passes. Bigger thread group size means that bigger islands can be processed without the need of writing temporary results to global memory.
Now, let’s discuss about the resource goals we must meet to run groups of 1024 threads efficiently:
- Registers: To saturate the GPU, each CU must be assigned two groups of 1024 threads. Given 65,536 available VGPRs for the entire CU, each thread may require, at maximum, 32 VGPRs at any one time.
- Groupshared memory: GCN has 64 KiB of LDS. We can use the full 32 KiB of groupshared memory and still fit two groups per CU.
If the shader exceeds these limits, there will not enough resources on the CU to run two groups at the same time. The 32 VGPR goal is difficult to reach. We will be first discussing the problems you face if you don’t reach this goal, and then solutions to solve this problem and finally how to avoid it altogether.
Problem: Single thread group per CU
Consider the case where an application uses the maximum group size of 1024 threads, but the shader requires 40 VGPRs. In this case, only one thread group per CU may execute at a time. Running two groups, or 2048 threads, would require 81,920 VGPRs – far more than the 65,536 VGPRs available on the CU.
1024 threads will yield 16 waves of 64 threads, which are distributed equally among the SIMDs resulting in 4 waves per SIMD. We learned earlier that optimal occupancy and latency hiding requires 10 waves, so 4 waves results in a mere 40% occupancy. This significantly reduces the latency hiding potential of the GPU, resulting in reduced SIMD utilization.
Let’s assume your group of 1024 threads is using the maximum of 32 KiB LDS. When only one group is running, 50% of LDS is not utilized as it is reserved for a second thread group, which is not present due to register pressure. Register file usage is 40 VGPRs per thread, for a total of 40,960 VGPRs, or 160 KiB. Thus, 96 KiB (37.5%) of each CU register file is wasted.
As you can see, maximum size thread groups can easily result in bad GPU resource utilization if only one group fits to a CU because we exceed our VGPR budget.
When evaluating potential group size configurations, it is important to consider the GPU resource lifecycle.
GPUs allocate and release all resources for a thread group simultaneously. Registers, LDS and wave slots must all be allocated before group execution can start, and when the last wave of the group finishes execution, all the group resources are freed. So if only one thread group fits on a CU, there will be no overlap in allocation and deallocation since each group must wait for the previous group to finish before it can start. Waves within a group will finish at different times, because memory latency is unpredictable. Occupancy decreases since waves in the next group cannot start until all waves in the previous group complete.
Large thread groups tend to use lots of LDS. LDS access is synchronized with barriers ( GroupMemoryBarrierWithGroupSync , link, in HLSL). Each barrier prevents execution from continuing until all other waves of the same group have reached that point. Ideally, the CU can execute another thread group while waiting on barriers.
Unfortunately, in our example, we only have one thread group running. When only one group is running on a CU, barriers limit all waves to the same limited set of shader instructions. The instruction mix is often monotonous between two barriers, and so all waves in a thread group will tend to load memory simultaneously. Because the barrier prevents moving on to later independent parts of the shader, there’s no opportunity for using the CU for useful ALU work that would hide the memory latency.
Solution: Two thread groups per CU
Having two thread groups per CU significantly reduces these problems. Both groups tend to finish at different times and hit different barriers at different times, improving the instruction mix and reducing the occupancy ramp down problem significantly. SIMDs are better utilized and there’s more opportunity for latency hiding.
I recently optimized a 1024 thread group shader. Originally it used 48 VGPRs, so only one group was running on each CU. Reducing VGPR usage to 32 yielded a 50% performance boost on one platform, without any other optimizations.
Two groups per CU is the best case with maximum size thread groups. However, even with two groups, occupancy fluctuation is not completely eliminated. It is important to analyze the advantages and disadvantages before choosing to go with large thread groups.
When large thread groups should be used
The easiest way to solve a problem is to avoid it completely. Many of the issues I’ve mentioned can be solved by using smaller thread groups. If your shader does not require LDS, there is no need to use larger thread groups at all.
When LDS is not required, you should select a group size between 64 to 256 threads. AMD recommends a group size of 256 as the default choice, because it suits their work distribution algorithm best. Single wave, 64 threads, groups also have their uses: GPU can free resources as soon as the wave finishes and AMDs shader compiler can remove all memory barriers as the whole wave is guaranteed to proceed in lock step. Workloads with highly fluctuating loops, such as the sphere tracing algorithm used to render our Claybook game, benefit the most from single wave work groups.
However, LDS is a compelling, useful feature of compute shaders that is missing from other shader stages, and when used correctly it can provide huge performance improvements. Loading common data into LDS once – rather than having each thread perform a separate load – reduces redundant memory access. Efficient LDS usage may reduce L1 cache misses and thrashing, and commensurate memory latency and pipeline stalls.
The problems encountered with groups of 1024 threads are significantly reduced when the group size is reduced. Group size of 512 threads is already much better: Up to 5 groups fit at one to each CU. But you still need to adhere to the tight 32 VGPR limit to reach good occupancy.
Neighborhood processing
Many common post-processing filters (such as temporal antialiasing, blurring, dilation, and reconstruction) require knowledge of an element’s nearest neighbors. These filters experience significant performance gains – upwards of 30% in some cases – by using LDS to eliminate redundant memory access.
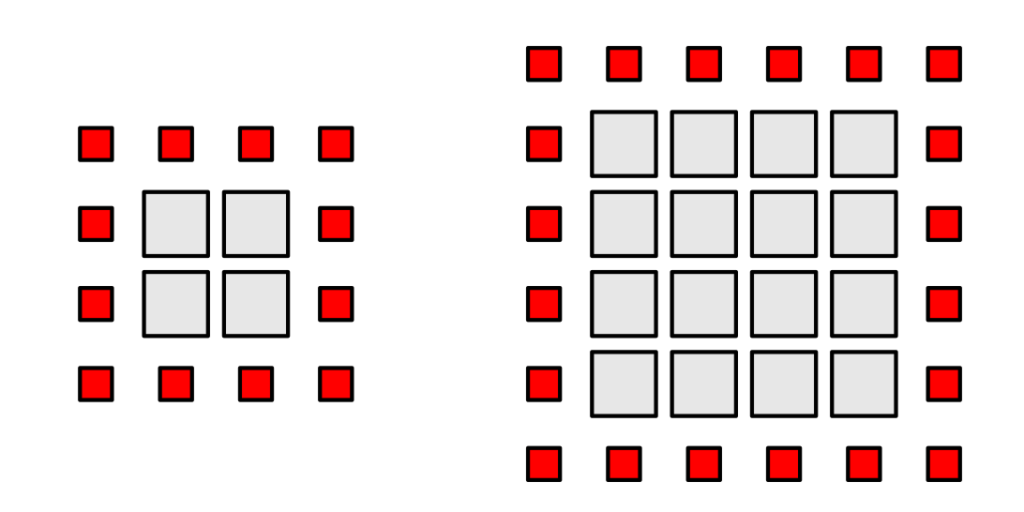
If we assume a 2D input, and that each thread is responsible for shading a single pixel, we can see that each thread must retrieve its initial value as well as the eight adjacent pixels. Each neighboring pixel will also require the thread’s initial value. Additionally, the center value is required by each neighboring thread. This leads to many redundant loads. In the general case, each pixel will be required by nine different threads. Without LDS, that pixel must be loaded nine times – once for each thread that requires it.
By first loading the required data into LDS, and replacing all subsequent memory loads with LDS loads, we significantly reduce the number of accesses to global device memory and the potential for cache thrashing.
LDS is most effective when there is a significant amount of data that can be shared within the group. Larger neighborhoods – and, therefore, larger group sizes – result in more data that can be meaningfully shared, and further reduces redundant loads.
Let us assume a 1-pixel neighborhood and a square 2D thread group. The group should load all pixels inside the group area and a one-pixel border to satisfy boundary condition requirements. A square area with side length X requires X^2 interior pixels, and 4X+4 boundary pixels. The interior payload scales quadratically, while the boundary overhead – pixels which are read, but not written to – scales linearly.
An 8×8 group with a one-pixel border encompasses 64 interior pixels and 36 border pixels, for a total of 100 loads. This requires 56% overhead.
Now consider a 16×16 thread group. The payload contains 256 pixels, with an additional overhead of 68 border pixels. Although the payload size is four times larger, the overhead is only 68 pixels, or 27%. By doubling the dimensions of the group, we have reduced overhead significantly. At the largest possible thread group size of 1024 threads – a square 32×32 neighborhood – the overhead of reading 132 border pixels accounts for a mere 13% of loads.
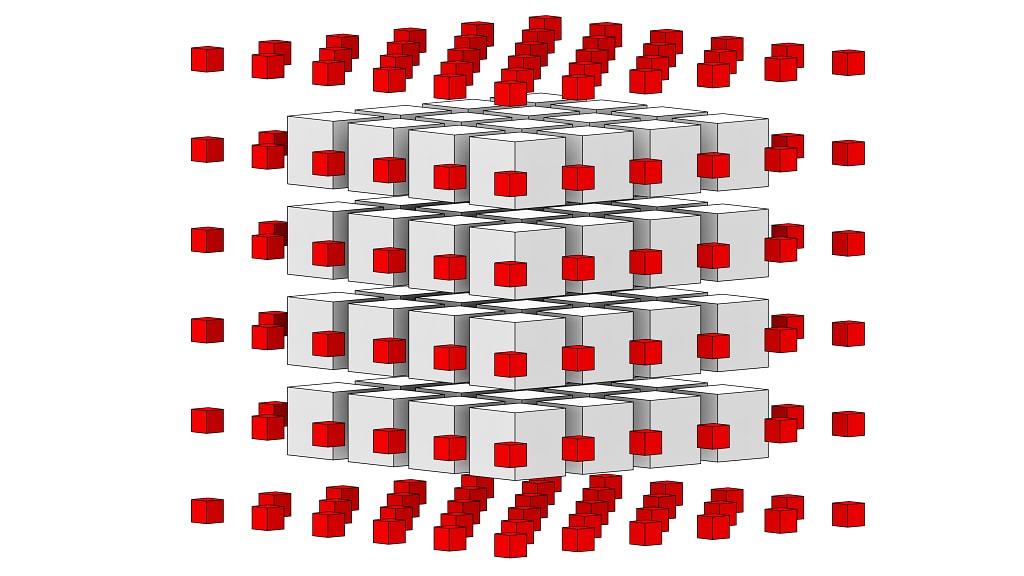
3D groups scale even better, since the group volume increases even faster than the boundary area. For a small 4x4x4 group, the payload contains 64 elements, while the surface boundary, an empty 6x6x6 cube, requires 216 elements, for an overhead of 70%. However, an 8x8x8 group with 512 interior pixels and a boundary area of 488 pixels requires 48% overhead. Neighbor overhead is huge for small thread group sizes, but improves with larger thread group sizes. Clearly, large thread groups have their uses.
Multi-passing with LDS
There are many algorithms that require multiple passes. Simple implementations store intermediate results in global memory, consuming significant memory bandwidth.
Sometimes each independent part, or “island,” of a problem is small, making it possible to split the problem into multiple steps or passes by storing intermediate results in LDS. A single compute shader performs all required steps and writes intermediate values to LDS between each step. Only the result is written to memory.
Physics solvers are a good application of this approach. Iterative techniques such as Gauss-Seidel require multiple steps to stabilize all constraints. The problem can be split into islands: all particles of a single connected body are assigned to the same thread group, and solved independently. Subsequent passes may deal with inter-body interactions, using the intermediate data calculated in the previous passes.
Optimize VGPR Usage
Shaders with large thread groups tend to be complex. Hitting the goal of 32 VGPRs is hard. Here are some tricks I have learned in the past years:
Scalar Data
GCN devices have both vector (SIMD) units, which maintain different state for each thread in a wave, and a scalar unit, which contains a single state common to all threads within a wave. For each SIMD wave, there is one additional scalar thread running, with its own SGPR file. The scalar registers contain a single value for the whole wave. Thus, SGPRs have 64x lower on-chip storage cost.
The GCN shader compiler emits scalar load instructions automatically. If it is known at compile time that a load address is wave-invariant (that is, the address is identical for all 64 threads in the wave), the compiler emits a scalar load, rather than having each wave independently load the same data. The most common sources for wave-invariant data are constant buffers and literal values. All integer math results based on wave-invariant data are also wave-invariant, as the scalar unit has a full integer instruction set. These scalar instructions are co-issued with vector SIMD instructions, and are generally free in terms of execution time.
The compute shader built-in input value, SV_GroupID , is also wave-invariant. This is important, as it allows you to offload group-specific data to scalar registers, reducing thread VGPR pressure.
Scalar load instructions do not support typed buffers or textures. If you want the compiler to load your data to SGPR instead of VGPR, you need to load data from a ByteAddressBuffer or StructuredBuffer . Do not use typed buffers and textures to store data that is common to the group. If you want to perform scalar loads from a 2D/3D data structure, you need custom address calculation math. Fortunately the address calculation math will also be co-issued efficiently as the scalar unit has a full integer instruction set.
Running out of SGPRs is also possible, but unlikely. The most common way to exceed your SGPR budget is by using an excessive number of textures and samplers. Texture descriptors consume eight SGPRs each, while samplers consume four SGPRs each. DirectX 11 allows using a single sampler with multiple textures. Usually, a single sampler is enough. Buffers descriptors only consume four SGPRs. Buffer and texture load instructions don’t need samplers, and should be used when filtering is not required.
Example: Each thread group transforms positions by a wave-invariant matrix, such as a view or projection matrix. You load the 4×4 matrix from Buffer using four typed load instructions. The data is stored to 16 VGPRs. That already wasted half of your VGPR budget! Instead, you should do four Load4 from a ByteAddressBuffer . The compiler will generate scalar loads, and store the matrix in SGPRs rather than VGPRs. Zero VGPRs wasted!
Unneeded Data
Homogeneous coordinates are commonly used in 3D graphics. In most cases, you know that W component is either 0 or 1. Do not load or use the W component in this case. It will simply waste one VGPR (per thread) and generate more ALU instructions.
Similarly, a full 4×4 matrix is only needed for projection. All affine transformations require at most a 4×3 matrix. Otherwise, the last column is (0, 0, 0, 1). A 4×3 matrix saves four VGPRs/SGPRs compared to a full 4×4 matrix.
Bit-packing
Bit-packing is a useful way to save memory. VGPRs are the most precious memory you have – they are very fast but also in very short supply. Fortunately, GCN provides fast, single-cycle bit-field extraction and insertion operations. With these operations, you can store multiple pieces of data efficiently inside a single 32-bit VGPR.
For example, 2D integer coordinates can be packed as 16b+16b. HLSL also has instructions to pack or extract two 16-bit floats to a 32-bit VGPR ( f16tof32 & f32tof16 ). These are full-rate on GCN.
If your data is already bit-packed in memory, load it directly to a uint register or LDS and don’t unpack it until use.
Booleans
The GCN compiler stores bool variables in a 64-bit SGPR, with one bit per lane in the wave. There is zero VGPR cost. Do not use int or float to emulate bools, or this optimization doesn’t work.
If you have more bools than can be accommodated in SGPRs, consider bit-packing 32 bools to a single VGPR. GCN has single-cycle bit-field extract/insert to manipulate bit fields quickly. In addition, you can use countbits() and firstbithigh() / firstbitlow() to do reductions and searching of bitfields. Binary prefix-sum can be implemented efficiently with countbits() , by masking previous bits and then counting.
Bools can also be stored in the sign bits of always-positive floats. abs() and saturate() are free functions on GCN – they are simple input/output modifiers that execute along with the operation using them — so retrieving a bool stored in the sign bit is free. Do not use the HLSL sign() intrinsic to reclaim the sign. This produces suboptimal compiler output. It is always faster to test if a value is non-negative to determine the value of the sign bit.
Branches and Loops
Compilers try to maximize the code distance from data load to use, so that memory latency can be hidden by the instructions in between them. Unfortunately, data must be kept in VGPRs between the load and the use.
Dynamic loops can be used to reduce the VGPR life time. Load instructions that depend on the loop counter cannot be moved outside of the loop. VGPR life time is confined inside the loop body.
Use the [loop] attribute in your HLSL to force actual loops. Unfortunately, the [loop] attribute isn’t completely foolproof. The shader compiler can still unroll the loop if the number of required iterations is known at compile time.
16 bit registers
GCN3 introduced 16 bit register support. Vega extends this by performing 16 bit math at double rate. Both integers and floating point numbers are supported. Two 16 bit registers will be packed into a single VGPR. This is an easy way to save VGPR space when you don’t need full 32 bit of precision. 16 bit integers are perfect for 2D/3D address calculation (resource loads/stores and LDS arrays). 16 bit floats are useful in post processing filters among other things, especially when you are dealing with LDR or post tonemapped data.
LDS
When multiple threads in the same group are loading the same data, you should consider loading that data to LDS instead. This can bring big savings in both load instruction count and the number of VGPRs.
LDS can also be used to temporarily store registers when they are not needed right now. For example: A shader loads and uses a piece of data in the beginning and uses that data again in the end. However the VGPR peak occurs in the middle of the shader. You can store this data temporarily to LDS and load it back when you need it. This reduces VGPR usage during the peak, when it matters.
Other posts by Sebastian Aaltonen
Optimizing GPU occupancy and resource usage with large thread groups
Sebastian Aaltonen, co-founder of Second Order Ltd, talks about how to optimize GPU occupancy and resource usage of compute shaders that use large thread groups.
Using Ryzen™ Threadripper for Game Development – optimising UE4 build times
Guest post by Sebastian Aaltonen, co-founder of Second Order. It covers optimising building the engine and asset production when using AMD Ryzen Threadripper processors.